Анализ генератора повышенной частоты

Анализ многоячейкового генератора повышенной частоты генератора удобно производить отдельно для установившегося и переходного режимов.

В установившемся режиме могут быть сделаны некоторые допущения, позволяющие вместо параллельного колебательного контура ввести эквивалентный генератор и тем самым понизить порядок системы дифференциальных уравнений, описывающих работу схемы.

Приближенный метод расчета генератора основан не только на обычных допущениях, указанных в главе первой, но также и на допущении, что затухание колебаний в контуре нагрузки за время между двумя соседними импульсами тока тиристоров мало, т. е. в контуре нагрузки происходят чисто синусоидальные колебания с постоянной амплитудой U_m и частотой ω.

При указанных допущениях контур нагрузки можно заменить эквивалентным источником ЭДС u_к (t) — U_{m sin} (ω_t + ψ), а тиристоры — идеальным ключом Кл.

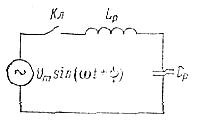Ключ Кл замыкается в момент отпирания одного из тиристоров схемы и размыкается в момент перехода его тока через нуль (т. е. в момент изменения направления тока). В результате эквивалентная схема генератора имеет вид, изображенный на рис. 5-11.

Рис. 5-11. Эквивалентная схема многоячеикового генератора повышенной частоты.

Дифференциальное уравнение рассматриваемой эквивалентной схемы

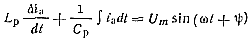(5-45)

В зависимости от выбора соотношений параметров разрядной цепи, контура нагрузки и частоты управляющих импульсов можно получить различные режимы работы генератора.

Для получения возможно более высоких частот необходимо, чтобы отношение амплитуды колебаний в контуре нагрузки U_m к абсолютному значению напряжения на емкости С_р после окончания протекания тока через тиристор (— U_Сра) было равно единице:

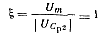(5-46)

При ζ>1 тиристоры лучше используются по мощности, однако на их анодах появляется положительное напряжение через время, меньшее периода генерируемой частоты (схемное время выключения мало), и высокие ни получены быть не могут.

Режим работы при ζ < 1 энергетически невыгоден, так как тиристоры хуже используются по мощности из-за роста на них максимального напряжения.

Рассматривая энергетические соотношения в генераторе, для схемы рис. 5-8 можно получить ряд важных выражений.

Изменение заряда емкости С_р за один цикл в результате протекания тока через тиристор (замыкания ключа кл) может быть выражено следующим образом:

q = C_р(U_Cp1-U_Cp2), (5-47)

где U_Сp1 и U_Сp1 — напряжения на емкости С_р в моменты начала и окончания протекания тока через тиристор.

Вводя коэффициент перезаряда емкости С_р

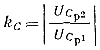(5-48)

получим

q = C_pU_Cp1(1+k_c). (5-49)

Учитывая выражения (5-48) и (5-49), энергию W_~, отдаваемую при перезаряде емкости С_р контуру нагрузки, можно определить из выражения

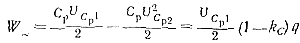(5-50)

Энергия W₀, отдаваемая источником питания Е₀ за один цикл, равна

W₀ = ∫E₀i_adt = E₀q (5-51)

Соотношения (5-50) и (5-51) позволяют выразить величину U_Cp1 через E₀ и k_C.

Поскольку источник питания отдает энергию один раз, при заряде емкости С_р через тиристор T₁, а энергия в контур нагрузки отдается дважды (тиристорами T₁ и Т₂), то, пренебрегая потерями в схеме, получим

U_Cp1=E₀ /(1-k_C). (5-52)

Зная напряжение U_Cp1 определяем максимальное напряжение на анодах тиристоров:

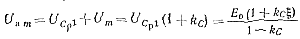(5-53)

Мощность, получаемая от генератора в пересчете на один тиристор, определяется выражением

P_~=W_~F_п (5-54)

Где F_п — частота повторения импульсов тока одного из тиристоров генератора.

Подставив в (5-54) выражения (5-50), (5-49) и значение U_Cp1, найденное из (5-53), получим

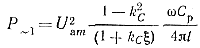(5-55)

где ω = 2πƒ— генерируемая частота; l= ƒ/F_п — коэффициент умножения частоты (для каждого из тиристоров).

Поскольку потери в схеме не учитываем, мощность, отдаваемая источником питания в пересчете на каждый тиристор, находится из выражения

Р₀₁=Е₀I₀₁≈P_~1(5-56)

где I₀₁ — постоянная составляющая тока через каждый тиристор.

Исходя из равенств (5-53), (5-55) и учитывая (5-56), можно получить соотношение

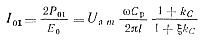(5-57)

из которого определяем

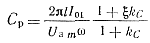(5-58)

Решая дифференциальное уравнение (5-45) с помощью преобразования Лапласа и учитывая, что начальное напряжение на емкости С_р равно U_Cp1, получим выражение для тока тиристоров:

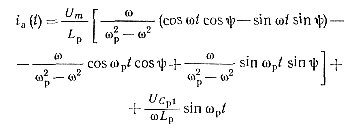(5-59)

где ω_p =1/√L_pC_p-собственная частота разрядной цепи L_pC_p; ω — частота генерируемых колебаний.

Вводя расстройку разрядной цепи относительно генерируемой частоты v = (ω_р—ω)/ω, безразмерное время τ= ω_t и используя выражения (5-46), (5-48), упростим выражение (5-59):

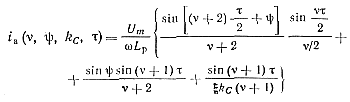(5-60)

Выключение тиристора происходит в момент τ₁, когда ток через него равен нулю:

i_a=(v, ψ, k_C, τ1) (5-61)

Напряжение U_Cp2 на емкости С_р в момент т, можно выразить через сумму напряжений u_к на контуре L_к, С_к, r_н и u_Lp  на индуктивности L_p согласно эквивалентной схеме (рис. 5-11):

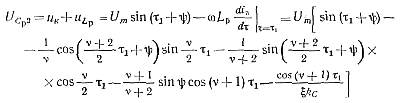(5-62)

Из уравнений (5-61) и (5-62) нетрудно исключить величину k_С, после чего с учетом того, что имеет место условие ζ= 1 [см. (5-46) ], для угла ψ получим уравнение вида

a sin ψ+b cos ψ = c

где

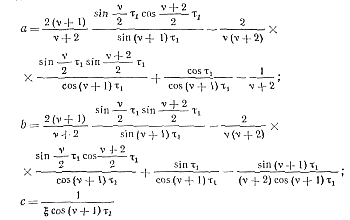(5-63)

Решая уравнение (5-63), получаем ψ в функции v, k_C и τ₁. Из уравнения (5-61) находим выражение для определения коэффициента k_C:

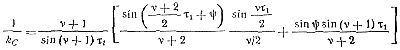(5-64)

К анодам тиристоров после окончания протекания через них тока прикладывается напряжение емкости С_р и контура нагрузки L_к, С_к, r_н, причем фаза напряжения на контуре нагрузки может быть различной.

Напряжение на аноде тиристора при его выключении изменяется либо плавно в соответствии с синусоидальным законом изменения напряжения на контуре нагрузки, либо скачкообразно.

Последнее нежелательно, так как возрастает обратный ток тиристора. Возрастание обратного тока, в свою очередь, приводит к увеличению потерь в тиристорах во время их выключения.

Поэтому для выбора режима работы генератора желательно знать скачок обратного напряжения на тиристорах после их выключения. Он равен напряжению U_Lp1 на индуктивности L_p в момент времени τ1.

Относительное значение его легко определить с помощью выражения (5-62):

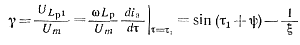(5-65)

Чтобы определить эквивалентное сопротивление и фазовый угол настройки контура нагрузки φ, необходимо найти синфазную (активную) I_1а и квадратурную (реактивную) I_1р составляющие первой гармоники тока i_a по отношению к ЭДС U_m sin(ωt+φ).

Используя выражение (5-60), получаем

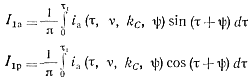(5-66)
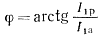(5-67)

По известным значениям I_1а и напряжения на контуре нагрузки находим эквивалентное сопротивление контура нагрузки:

R_э= U_m/I_1a (5-68)

Постоянную составляющую тока одного тиристора I₀₁ определим по выражению

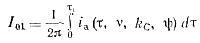(5-69)

Максимальный ток через тиристор I_аm определяется из выражения (5-60) при подстановке в него вместо τ величины τ_м — времени достижения током тиристора максимального значения, которое определяется из уравнения

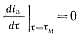(5-70)

Имея выражения для величин I_аm, I_1а, I₀₁, легко найти коэффициенты, позволяющие связать эти величины между собой, аналогичные коэффициентам разложения в ряд Фурье импульса анодного тока в теории ламповых генераторов:

a₁ = I_1a/l/(2I_amm); а₀ = I_01l/I_ам, (5-71)

где m — число пар тиристоров, а_l — коэффициент умножения частоты, введенный ранее.

Полученные выражения позволяют определить величины k_C, τ₁, ψ, γ, v, a₁, a₀, φ, необходимые для расчета генератора. Анализ режимов работы генератора показал, что наилучшим с практической точки зрения является режим работы, при котором частоты настройки контура нагрузки и импульсов управления тиристоров кратны.

При этом настройка генератора может производиться по минимуму потребляемого от источника питания тока (аналогично ламповым генераторам с независимым возбуждением).

В случае импульсной работы генератора переходные процессы установления частоты и фазы в начале радиоимпульса отсутствуют. Напряжение на разрядной индуктивности L_p в момент oкончания импульса тока в оптимальном режиме целесообразно положить равным нулю.

При этом условии и принятом ранее значении ζ = 1 напряжение на аноде тиристора после окончания протекания тока изменяется плавно, без скачков, которые могут вызвать паразитные колебания в разрядных цепях L_pС_p, приводящие к дополнительным потерям и перенапряжениям на элементах этих цепей и анодах тиристоров.

Скачкообразное приложение к тиристору обратного напряжения после окончания протекания прямого тока приводит, кроме того, к появлению значительного обратного тока тиристора и увеличивает потери при выключении.

Для оптимального режима получены следующие значения параметров: τ2=276°, ψ = 174°, v = — 0,135, k_C = 0,422, а₁ = 0,510, а₀ = 0,370.

Для анализа процессов установления колебаний в генераторе при его включении (переходный режим) необходимо решать системы дифференциальных уравнений для отдельных этапов работы схемы (открывания или закрывания тиристоров), считая конечное состояние системы в конце этапа начальным состоянием для последующего этапа.

Решение системы дифференциальных уравнений для отдельных этапов можно осуществить либо интегрированием с помощью хорошо известных методов на ЭВМ, либо используя преобразование Лапласа.

Второй способ позволяет получить аналитические выражения для токов и напряжений в схеме на отдельных этапах ее работы, но они оказываются столь сложного вида, что практическое их использование весьма затруднительно.

Кроме того, при реализации этого способа предварительно необходимо определить корни характеристического уравнения четвертой степени общего вида.

Максимальные значения токов и напряжений в схеме во время переходного процесса можно получить путем анализа процесса включения.

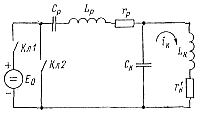Делая те же предположения, что и ранее, можно составить эквивалентную схему генератора (рис. 5-12), в которой ключи Кл1 и Кл2 отображают соответственно тиристоры Т1 и Т2, ЭДС Е0 — источник питания, сопротивление rр — потери в разрядной цепи, сопротивление r'н — потери в контуре нагрузки с учетом сопротивления нагрузки rн, пересчитанного как последовательно включенное с индуктивностью Lк и емкостью Ск.

Рис. 5-12. Эквивалентная схема для анализа переходных процессов в многоячейковом генераторе повышенной частоты

Каждый период работы схемы можно разбить на четыре этапа.

Первый этап начинается с приходом импульса управления на тиристор Т₁, т. е. с момента замыкания ключа Кл₁ (ключ Кл₂ при этом разомкнут). Согласно эквивалентной схеме, на этом этапе работа генератора может быть описана системой двух интегродифференциальных уравнений:

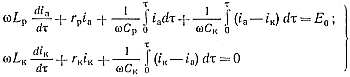(5-72)

Здесь τ = ω_t — безразмерное время.Начальные условия — нулевые (напряжения на емкостях схемы и токи в схеме равны нулю):

U_cp(01)-u_Cк(0); i_a(0)=i_к(0)=0

Далее преобразуем систему иитегродифференциальных уравнений (5-72) в систему дифференциальных уравнений, для которых существует хорошо разработанные и широко известные методы решения с помощью ЭВМ. Это преобразование осуществляется заменой переменных:

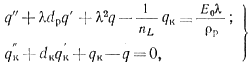(5-73)

После замены и простых преобразований система уравнений (5-72) записывается в виде

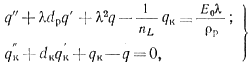(5-74)

где q', q'_к и q", q"_к —соответственно первая и вторая производные переменных q и q_к; d_к = r'_н(ωL_к) — затухание контура нагрузки; ρ_р — волновое сопротивление цепи L_p, С_р; d_p=r_р/(ω_pL_p) — затухание разрядной цепи L_p, С_р; r_p; λ = ω_p/ω — отношение частот разрядной цепи ω_р = 1/√L_pC_p и контура нагрузки ω = ω_к =  1/√L_кC_к; n_L=L_к/L_p — отношение индуктивностей контypa нагрузки и разрядной цепи.

Считаем, что имеет место оптимальный режим работы генератора. Интегрируя с помощью ЭВМ систему уравнений (5-74), определим максимальное значение тока через тиристор на данном этапе I_am1 и момент окончания тока τ₁₁ т.е. момент размыкания ключа Кл₁, что соответствует окончанию первого этапа.

Для момента τ₁₁ найдем значения q(τ₁₁), q_к(τ₁₁) и q'(τ₁₁), являющиеся начальными условиями для второго этапа.

С момента окончания протекания тока через тиристор Т₁ (размыкания ключа Кл₁) до момента поступления импульса управления на тиристор Т₂ при τ₂₁ = 2πj длится второй этап.

Величина j= 1, 2, 3 .. . означает номер периода частоты следования импульсов тока тиристоров через контур нагрузки, и для первого рассматриваемого периода она равна 1.

Однако для общности записи дальнейших выражений величину j сохраним. Во время второго этапа ток i_a равен нулю, а в контуре нагрузки имеют место свободные колебания, описываемые уравнением

q"_к + dкq'_к+q_к = 0. (5 -75)

Решая это уравнение при начальных условиях d_к (0) = d_к (τ11) и q'_к (0) = q'_к (τ11), находим эти величины для второго этапа:

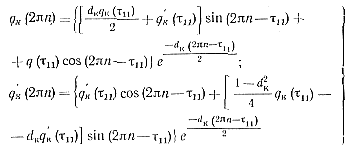(5-76)

Находя значения величин в момент окончания этапа n = j, получим начальные значения для третьего этапа:

q(0) =q(2πj);  q_к(0) =q_к(2πj); q'_к(0) =q'_к(2πj).   (5-77)

Третий этап соответствует замкнутому состоянию тиристора Т₂ (ключа Кл₂ на рис. 5-12).

Процессы, протекающие во время этого этапа, аналогичны процессам во время первого этапа и тоже описываются системой двух иитегродифференциальных уравнений, но однородной:

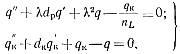(5-78)

Так же, как и на первом этапе, определяем величину I_am2, момент окончания тока τ₁₂ и значения q (τ₁₂), q_к (τ₁₂), q'_к (τ₁₂).

На четвертом этапе оба ключа снова разомкнуты, i_а = 0, в контуре нагрузки существуют свободные колебания, описываемые уравнением (5-75), но с другими начальными условиями, определенными при анализе третьего этапа.

Решая это уравнение, находим начальные условия для момента прихода следующего импульса управления.

Следующий импульс управления снова замыкает ключ Кл₁, т. е. начинается второй период работы схемы, но на первом этапе второго периода начальные условия уже не нулевые, а определяются четвертым этапом предыдущего периода.

Далее вычисления производятся аналогично описанным для первого периода. Процедура повторяется для р периодов до получения установившегося режима.

На каждом этапе проводимости тиристоров, определив значения q (τ1j), q_к (1j) и q'_к (1j), можно найти амплитуду колебательного напряжения на контуре L_к, С_к

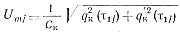(5-79)

фазу его

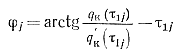(5-80)

и напряжение на аноде тиристора после окончания протекания через него тока

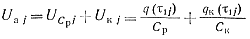(5-81)

Доведя вычисления до установившегося режима, можно определить время установления процесса, максимальные напряжения на анодах тиристоров и контуре нагрузки и максимальный ток через тиристоры в переходном процессе (U_{am max}, U_mmax, I_amax).

Процесс считаем законченным, когда максимальное напряжение на аноде U_amj отличается от своего установившегося значения меньше чем на 3 %.

Схемное время выключения при анализе переходных процессов не вычисляется, так как в основном, как будет видно из дальнейшего, определяется частотой включения отдельных тиристоров схемы. Поэтому малое изменение его во время переходного процесса практического значения не имеет.

Длительность переходных процессов и превышение максимальных значений токов и напряжений для тиристоров, а также напряжения на контуре нагрузки вычисляется изложенным способом в функции добротностей разрядной цепи Q_p = √L_p/C_p/r_p и контура нагрузки Q_к = r_н/√L_к/С_к и коэффициента умножения частоты l = ƒ/F_п.

На рис. 5-13 — 5-15 даны зависимости относительных максимальных значений напряжений Vc_p1m на емкости С_р и U_mmaх на контуре нагрузки, тока тиристора I_аmmах в переходном процессе.

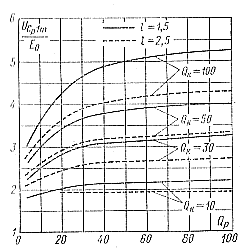Рис. 5-13. Зависимости для максимального напряжения на конденсаторе Ср

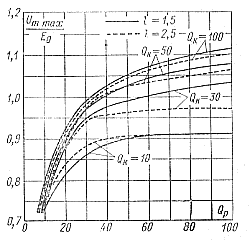Рис. 5-14. Зависимости для максимального напряжения на контуре нагрузки

Величина U_{am mах} определяется как U_{a max} = U_C1m+U_mmax. Из рисунков видно, что приведенные величины возрастают с увеличением добротностей Q_p и Q_к и уменьшением коэффициента l.

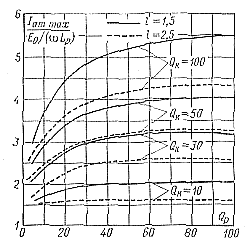Первое объясняется уменьшением потерь в колебательной цепи, а второе — меньшими промежутками между поступлениями энергии в колебательную систему. Длительность переходного процесса в периодах для больших добротностей разрядного контура Qp = 50 и контура нагрузки Qк= 50 и 100 соответственно равна 8 и 14. При уменьшении Qp и Qк длительность переходного процесса уменьшается.

Рис. 5-15. Зависимости для максимального тока через тиристоры

Расчет генератора на максимальную мощность при заданной частоте ƒ = 1/Т и известных параметрах тиристоров удобно производить следующим образом:

1. При выборе коэффициента умножения частоты l следует исходить из того, что схемное время выключения должно превосходить номинальное. Схемное время выключения можно связать с периодом колебаний генерируемой частоты неравенством

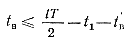(5-82)

где t'_в — время от момента включения второго тиристора в ячейке до изменения знака напряжения на аноде первого тиристора (см. рис. 5-9); t₁ — время, когда тиристор открыт.

Величина обычно для всех случаев много меньше lT/2 и t₁ и поэтому ею можно пренебречь.

Исключение составляет случай использования одной ячейки при l = 1. Однако он на практике встречается редко.

Тогда, учитывая, что для оптимального режима t₁≈ 0,75 T, получим

t_в≤(l/2-0,75)T (5-83)

Отсюда найдем

l≥2t_в/Т+3/2 (5-84)

Неравенство (5-84) позволяет определить число l, подставляя в качестве t_в величину t_в.ном. За величину l принимается наименьшее целое число, большее величины 2t_в/Т+ 3/2.

2. Для того чтобы определить число ячеек в генераторе, следует найти неравномерность амплитуды колебаний в контуре нагрузки, определяемую добротностью этого контура.

Так как затухание колебаний между двумя ближайшими импульсами тока тиристоров через контур L_к, С_к, r_н происходит по экспоненциальному закону, то неравномерность колебаний ε определяется отношением

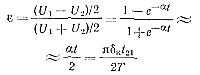
где t₂₁—время между окончанием предыдущего и началом следующего импульса тока через тиристоры; δ_к=Δω/ω — затухание контура L_к, С_к, r_н (Δω—ширина полосы пропускания); U₁— амплитуда напряжения на контуре нагрузки в момент окончания импульса тока через один из тиристоров; U₂ — амплитуда напряжения на контуре нагрузки в момент начала следующего импульса тока через тиристоры.

Зная допустимые значения ε и φ_к, легко определить время t_2l. Оно должно удовлетворять неравенству

t₂₁≤lT/2-t₁

Если получаем t₂₁>lT/2—t₁, то надо вместо одной ячейки взять большее число ячеек, чтобы добиться выполнения требуемого неравенства.

3. Учитывая, что в оптимальном режиме а₀ = 0,37, и полагая I_am=I_amд, найдем выражение для постоянной составляющей тока каждого тиристора:

I₀1=a₀I_am/l (5-85)

При использовании пары тиристоров (см. рис. 5-8) или нескольких пар импульсы тока, возбуждающего контур L_к, С_к, r_н следуют с частотой mFп/2 (где m — число ячеек в генераторе), поэтому для активной составляющей первой гармоники тока через контур нагрузки получаем выражение

I_1а = m_a1I_am/l= m_a1I₀₁/а₀. (5-86)

4. С помощью выражения (5-58) определяем С_р, после чего нетрудно найти индуктивность разрядной цепи:

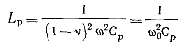(5-87)

5. Из выражения (5-53) следует найти E₀, полагая U_ammax = U_a.д, после чего с помощью выражений (5-52) и (5-53) определяем

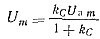  (5-88)

6. Зная величины U_m и I_1а, нетрудно найти R_э=U_m/I_1a
7. Поскольку КПД принят равным 100 %, получаем P_~=P₀=U_mI_1a/2.
8. Необходимо проверить, не превосходит ли крутизна тока тиристора допустимого значения.

Для этого, полагая, что ток через тиристоры нарастает до значения I_аm/2 по закону, близкому к линейному, получим выражение для крутизны нарастания тока:

S_i = I_аmω/(2r'),

где r' — время, в течение которого ток ia возрастает до значения I_am/2.

Как и для последовательного инвертора, возможен мостовой вариант схемы, который при необходимости может содержать несколько ячеек, работающих на общую нагрузку.