Расчет схемы последовательного инвертора

Рассмотрим основные уравнения последовательного инвертора на примере симметричной схемы, полагая, что сопротивление z_н чисто активное и равно r_н. Индуктивности L₁, L₂ равны L, и оба тиристора инвертора работают в одинаковых условиях.

Ранее говорилось, что при включении тиристора T₁ в момент t= 0 начинается заряд емкости С₁ через цепь r_н, L₁ от верхнего источника питания E₀/2. С помощью теоремы об эквивалентном генераторе напряжения цепь заряда может быть заменена последовательно соединенными эквивалентным генератором напряжения, индуктивностью L, емкостью С₁ и нагрузкой r_н.

Эквивалентная ЭДС равна напряжению на аноде тиристора u_а1 в момент t = 0, т. е. величине U_am, и представляет собой сумму напряжения источника питания E₀/2 и начального напряжения на емкости u_c‌ t=0.

u_a1‌ t₀=U_am=E₀/2+u_c‌ t=0(3-34)

Лапласово преобразование для тока тиристора i_a имеет вид

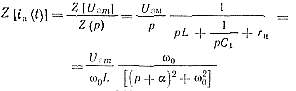(3-35)

где L = L₁ = L₂; α= r_н/(2L) — коэффициент затухания;  ω₀ =√₁/(LC₁)-α₂ —частота свободных колебаний контура L, С₁, r_н.

Используя обратное преобразование Лапласа, получим выражение для тока

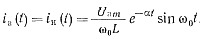(3-36)

Напряжение //L на индуктивности L_x равно

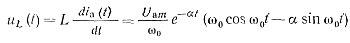(3-37)

В момент t₂= π/ω₀ ток i_a прекращается. Напряжение на индуктивности L₁ в момент окончания тока равно u_L‌ t=t₂=π/ω₀, а напряжение на аноде скачком изменяется на такую же величину и остается неизменным до момента t₃ включения тиристора T₂ (см. рис. 3-7):

u_a1‌ t=t₃=u_L‌ t=t₂=π/ω₀=-U_ame-πα/ω₀. (3-38)

Для тиристора T₂ момент t=t₃ является начальным и напряжение на его аноде в установившемся режиме должно быть таким же, как у тиристора T₁ в момент t= 0.

При выключенных тиристорах получаем

u_a2‌ t=t₃=E₀-u_La1‌  t=t₃=u_a1‌ t=0 (3-39)

Подставляя в уравнение (3-39) значения u_а1|t=0 из выражения (3-34) и u_a1‌ t=t₃ из (3-38), можно найти

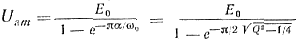(3-40)

где Q₂ = L/(C1r²_н) — добротность контура L, С₁, r_н на частоте его собственных колебаний ω₀.

Постоянная составляющая тока тиристора определяется по известной формуле

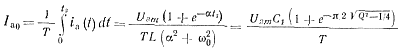(3-41)

Из выражения (3-37) видно, что производная тока i_a обращается в нуль в момент t=t_м = arctg (ω₀/α)/ω₀.

Вводя безразмерное время τ=ω₀t, получим

τ_м=ω₀tм=arctg 2√/Q2-¼.Отсюда максимальное значение тока

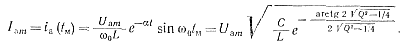(3-42)

На повышенных частотах значение тока через тиристоры может ограничиваться допустимой скоростью нарастания его, т. е. крутизной. Последняя максимальна в момент t=0 и согласно выражению (3-36) равна

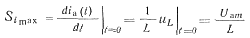(3.43)

В течение времени от t₃ до t₅ (см. рис. 3-7) емкость С₁ перезаряжается через тиристор Т₂. При этом существует зависимость u_a1 = Е₀—uL. Из-за равенства L₁ = L2 = L напряжение на индуктивности L₂ в интервале времени t₃—t₅ идентично напряжению на индуктивности L₂ в интервале от нуля до t₂.

Отрезок времени t_3,4 =t₃—t₄, когда напряжение на аноде тиристора отрицательно, определяется из условия u_L = E₀, которое на основании выражений (3-37) и (3-40) может быть представлено в виде

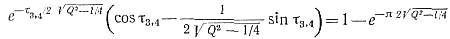(3.44)

Момент t₄ определяется из условия u_а1 = 0 или u_L = E₀. Решив это уравнение, можно найти зависимость величин

τ_3,4=ω₀t₃,4=γωt_3,4 и t_3,4/T₀=ω₀t_3,4/(2π) (3-45)

от параметров Q и γ, где γ=ω₀/ω; Т₀ = 2π/ω₀.

Отрицательное напряжение на аноде тиристоров сохраняется не только в течение времени t_3,4, но и от момента времени t₂ до момента t₃. Этот отрезок времени t_2,3 = t₃—t₂ определяется выражением

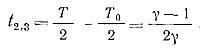  (3-46)

С помощью выражений (3-45) и (3-46) находим коэффициент k_в:

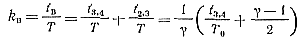  (3-47)

При включении инвертора нарастание максимальных значений тока через тиристоры и напряжения на них, как показывают расчеты, происходит монотонно и не может привести к нарушению устойчивости работы инвертора.

Поэтому для обеспечения устойчивой работы достаточно учитывать уменьшение времени выключения t_в в течение переходного процесса.

Поскольку минимальное время t_{в. min}, предоставляемое для выключения тиристора, как показали вычисления, имеет место в первом периоде работы инвертора, то его и следует определить ( t_{в. min} = t_в1).

Для этого найдем напряжение на аноде тиристора Т₁ в момент его запирания во время первого периода работы инвертора. Это можно сделать с помощью выражения (3-38), учитывая, что вместо величины U_аm следует подставить Е₀/2:

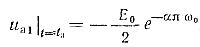(3.48)

Затем, используя зависимость u_a2‌ t=t₃=E₀-u_a1‌ t=t₃ и выражения (3-37), (3-38), определим

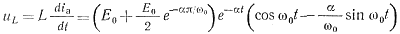(3-49)

Для момента t= t₄ имеем u_a1‌ t=t₄=E₀-u_L‌ t=t₄=0, следовательно, с помощью выражения (3-49) можно получить уравнение для определения безразмерного времени τ_3,4 = (t₄—t₃) ω₀ в первом периоде:

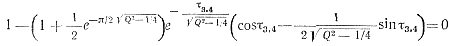(3-50)

Величину t_{в. min} легко определить в функции параметров Q и γ на основании выражения (3-47).

Учитывая, что в общем виде напряжение на аноде первого тиристора в момент его включения, соответствующий началу периода работы инвертора, определяется выражением

u_a1‌ t=0=E₀-u_a2‌ t=t₅=E₀-u_L‌ t=t₅

а напряжение на аноде второго тиристора в момент его включения, соответствующий середине периода работы инвертора,— выражением

u_a2‌ t=t₃=E₀-u_a1‌ t=t₃=E₀-u_L‌ t=t₂,

и используя выражения (3-37), (3-38), (3-48), получим рекуррентную формулу для определения максимального напряжения на анодах тиристоров в течение переходного процесса:

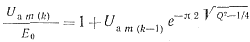  (3-51)

где U_am(k)— максимальное напряжение на аноде тиристора для k-го полупериода. В частности, для первого полупериода U_am (k)/E₀ = 0,5.

Длительность переходного процесса в периодах k' в зависимости от добротности Q легко оценить с помощью выражения (3-51). Вычисления показывают, что число k' с достаточной степенью точности равно добротности Q.

Анализ полученных результатов показывает, что с увеличением добротности Q ухудшается использование тиристоров и по току и по напряжению. Коэффициент использования тиристора по мощности можно определить с учетом выражений (3-40), (3-41), (3-42):

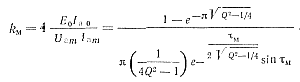  (3-52)

Вычисленные величины k_в, t_вmin/t_в, k_м приведены в табл. 3-2. Выражения для остальных величин, определяющих режим работы инвертора, достаточно просты и не требуют предварительных вычислений.

Таблица 3-2

Величина k_в, являющаяся частотным критерием инвертора, увеличивается с ростом Q причем особенно существенно при Q = 1÷3. Зависимость t_вmin/t_в от параметров Q и γ показывает, что чем меньше Q и больше γ, тем меньше отличается t_{в min} от времени выключения в установившемся режиме.

На основании сказанного можно сделать вывод, что на низких частотах, где нетрудно получить t_{в min} больше номинального времени выключения тиристоров t_в.ном, следует выбирать добротность Q = 1÷2, при которой значения k_м возрастают.

Однако с ростом генерируемой частоты величину Q нужно выбирать большей, чтобы обеспечить большие значения t_{в min}.

Увеличение параметра у более 1,5 ведет к значительному увеличению искажений выходного напряжения из-за прерывистости тока тиристоров.

Расчет инвертора на максимальную мощность по заданным параметрам тиристоров и частоте колебаний в нагрузке ƒ= l/Т удобно производить в следующем порядке:

1. Из соображений, приведенных выше, и из условия t_{в min}≥t_в.ном выбираем режим работы инвертора (т. е. величины Q и γ).
2. С помощью формулы (3-40) находим Е₀ по известному значению U_a.д.
3. Поскольку величина ƒ задана, a Q и γ определены при выборе режима работы, то находим собственную частоту ω₀=ωγ контура LC₁r_н, затухание 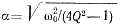и произведение LC₁.
4. По одной из формул (3-42) или (3-43) найдем либо величину С₁ либо √L/C₁, зная которые, вычисляем L и r_н. Выбор той или иной формулы определяется тем, какая величина ограничивает использование тиристоров инвертора: I_аmд или S_iд.

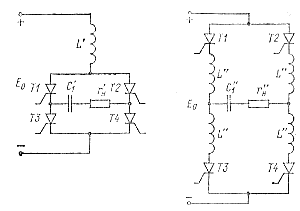Если нагрузка инвертора имеет активно-индуктивный или активно-емкостный характер, то в первом случае индуктивность становится частью индуктивности L коммутирующего контура, а во втором инвертор преобразуется в последовательно-параллельный, рассматриваемый в следующем параграфе. Реактивная составляющая нагрузки может быть также компенсирована реактивностью противоположного знака, в результате чего инвертор становится резонансным. В ряде практических случаев получила распространение мостовая схема последовательного инвертора, две модификации которой изображены на рис. 3-9.

Рис. 3-9. Мостовые схемы последовательных инверторов

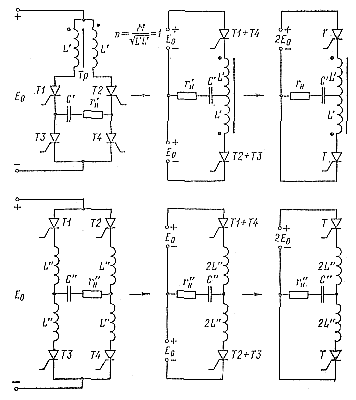С помощью эквивалентных преобразований, представленных на рис. 3-10, можно показать, что мостовые схемы эквивалентны полумостовым схемам, изображенным на рис. 3-6. Из сравнения мостовых и иолумостовых схем следует, что для получения одинаковых мощностей в нагрузках r'н и r"н при неизменном напряжении источника питания Е0 необходимо положить C'1= С"1 = С1/4; L' =2L"= 4L; r'н = r"н = 4rн. При этом в мостовых схемах токи через каждый тиристор уменьшаются вдвое, а максимальное напряжение на аноде тиристора, ток, потребляемый от источника питания E0, и, следовательно, потребляемая мощность останутся неизменными.

Сравнивая схемы, изображенные на рис. 3-9, следует отметить, что поскольку они эквивалентны схемам на рис. 3-6, им соответственно присущи недостатки и положительные качества последних.

В первой схеме рис. 3-9 максимальное напряжение на анодах тиристоров выше, чем во второй схеме, а схемное время выключения несколько больше.