При расчёте схемы последовательно-параллельного инвертора с удвоением частоты используются условия: L1 = L2 = L3 = L4 = L, C1 = C2 = C3 = C4 = С, нагрузка — активная.
Могут быть выделены два этапа работы схемы: первый, когда один из тиристоров включен, и второй, когда все тиристоры выключены.
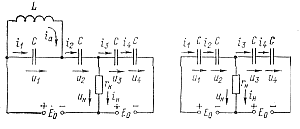 |
Эквивалентная схема для первого этапа, когда, например, включен тиристор Т1, представлена на рис. 5-6 слева. Для нее справедливы следующие уравнения (5-30):
|
где q1=Cu1; q2=Cu2; q3=Cu3; q4=Cu4;— заряды соответствующих емкостей, а обозначении других величин показаны на рис. 5-6.
Из уравнений (5-30) легко получить преобразованное по Лапласу выражение для тока ia:
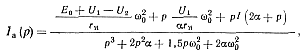 (5-31)
(5-31)
где α = l/(2rнС); ω0 = 1√/2LC; U1, U2, I — начальные для данного этапа значения величин u1, u2, iа.
После обратного преобразования получаем
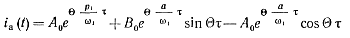 (5-32)
(5-32)
где τ = ωt — безразмерное время; ω — удвоенная частота управляющих импульсов каждого тиристора, равная частоте колебаний в нагрузке;
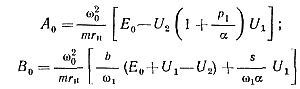
p1; Р2=А+Jω1; Р3=а-jω1 — корни уравнения для выражением в знаменателе (5-31); b = a—р1; m= b2 + ω21; s= ω21+ab; Θ=ω1/ω - относительная расстройка.
С помощью выражений (5-30) могут быть также получены зависимости для напряжении u1, u2, u3, u4 и uн в схеме:
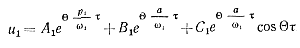 (5-33)
(5-33)
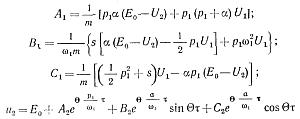 (5-34)
(5-34)
где
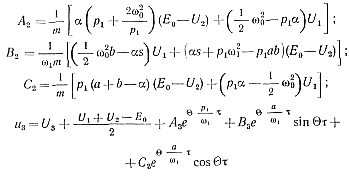 (5-35)
(5-35)
где
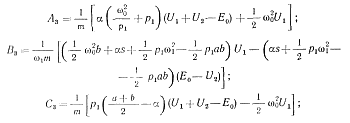
U3— начальное значение величины u3 для данного этапа;
u4 = u3 + U3-U4, (5-36)
где U4 — начальное значение величины u4 для данного этапа;
uн= E0— u1—u2 (5-37)
После окончания протекания тока через тиристор Т1 наступает второй этап работы схемы, когда ни один из тиристоров не включен. Эквивалентная схема для данного этапа изображена на рис. 5-6 справа.
Процессы в ней могут быть описаны уравнениями:
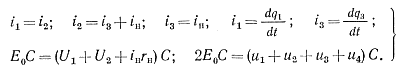 (5-38)
(5-38)
Из уравнений (5-38) нетрудно найти выражения для напряжений u1, u2, u3, u4, uн на втором этапе:
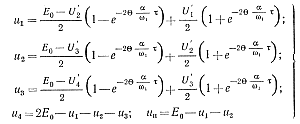 (5-39)
(5-39)
где U'1, U'2, U'3, U'4 — начальные значения напряжений u1, u2, u3, u4 на данном этапе.
Следует помнить, что отсчет времени в выражениях (5-39) производится с момента выключения одного из тиристоров (например, T1).
Выражения для величин U'1, U'2,U'3, U'4 получаются при подстановке в формулы (5-33) — (5-36) значения безразмерного времени τ0 протекания тока через тиристоры (τ0 = ωt0):
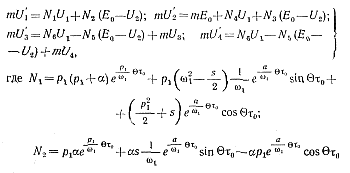 (5-40)
(5-40)
При подстановке в формулы (5-39) значения τ= π—τ0 получим выражения для напряжений u1, u2, u3, u4 в моменты отпирания тиристоров в любой k-й полупериод работы инвертора:
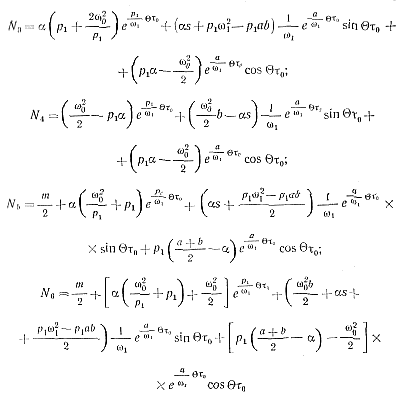 (5-40)
(5-40)
В частности, для установившегося режима U1k=U1; U2k=U2; U3k=U3; U4k=U4. Используя эти равенства, из выражении (5-40) и (5-41) нетрудно найти величины U1, U2, U3, U4:
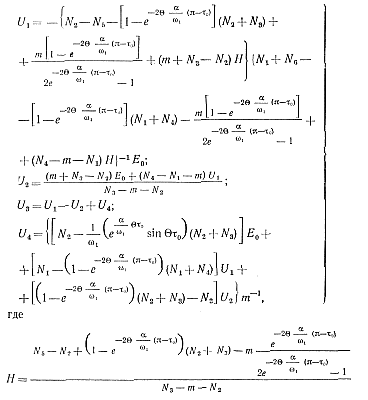 (5-42)
(5-42)
Дальнейшие вычисления величин, описываемых полученными выражениями, производятся в функции волнового сопротивления ρ = √l/(2C), добротности Q=ρ/rн и параметра Θ.
Величина τ0, как следует из полученных ранее выражений, в частности (5-32) и (5-42), является функцией величин U1 и U2.
Соответственно для нахождения τ0 могут быть пользованы уравнения, полученные из выражения (5-32) подстановкой в него величины τ0, и выражения (5-42). Вычисления показали, что все значения произведения Θτ0 при 0,1≤Q≤3 находятся в сравнительно узком интервале (π≤Θτ≤1,05π).
Напряжения U1, U2, U3, U4 вычисляются с помощью выражений (5-42), максимальный ток тиристоров Uam - c помощью (5-35), а максимальное напряжение на анодах запертых тиристоров Uam - помощью (5-35).
Действующее значение и коэффициент гармоник напряжения на нагрузке определяются из выражений
Таблица 5-3
|
Вычисляемая величина |
Q |
λ | |||
|
1.028 |
1.194 |
1.388 |
1,668 | ||
|
τ0 |
0,1 |
3,07 |
2.56 |
2,27 |
1,90 |
|
0,2 |
3,07 |
2.66 |
2,30 |
1.92 | |
|
0,3 |
3,08 |
2,68 |
2,33 |
1,95 | |
|
0,5 |
3,10 |
2,70 |
2,35 |
1,97 | |
|
0,7 |
3,09 |
2,69 |
2,33 |
1,94 | |
|
1,0 |
3,08 |
2,66 |
2,30 |
1,91 | |
|
1,25 |
3,07 |
2,65 |
2,28 |
1,90 | |
|
1,5 |
3,06 |
2,64 |
2,27 |
1,89 | |
|
2,0 |
3.06 |
2,63 |
2,27 |
1,89 | |
|
3,0 |
3,06 |
2.63 |
2,26 |
1,88 | |
|
|
0,1 |
11,68 |
8,98 |
7,08 |
5.47 |
|
0,2 |
6,38 |
4,97 |
4,01 |
3,22 | |
|
0,3 |
4,73 |
3,78 |
3,15 |
2,65 | |
|
0,5 |
3,68 |
3,11 |
2,76 |
2,52 | |
|
0,7 |
3,52 |
3,13 |
2,91 |
2,80 | |
|
1,0 |
3,84 |
3,56 |
3,46 |
3,42 | |
|
1,25 |
4,28 |
4,07 |
4,01 |
4,12 | |
|
1,5 |
4,80 |
4,63 |
4,59 |
4,58 | |
|
2,0 |
5.94 |
5,82 |
5,80 |
5,80 | |
|
3,0 |
8.36 |
8,29 |
8,29 |
8,23 | |
|
|
0,1 |
—3,41 |
—2.67 |
—2,14 |
— 1,69 |
|
0,2 |
—1.79 |
—1,48 |
—1,27 |
—1,10 | |
|
0,3 |
— 1,39 |
—1,24 |
—1,14 |
— 1,06 | |
|
0,5 |
—1,37 |
—1,35 |
—1,34 |
— 1,33 | |
|
0,7 |
—1,67 |
— 1,70 |
—1,72 |
— 1,73 | |
|
1,0 |
—2,30 |
—2,36 |
—2,39 |
—2,40 | |
|
1,25 |
—2.88 |
—2,96 |
—2,98 |
—3,00 | |
|
1,5 |
—3,49 |
—3,56 |
—3,57 |
—3,58 | |
|
2,0 |
—4.72 |
—4.79 |
—4,80 |
—4,80 | |
|
3,0 |
—7,24 |
—7,28 |
—7,29 |
—7,23 | |
|
kг |
0,1 |
0,7 |
5.2 |
10,0 |
16,3 |
|
0,2 |
1.0 |
5,2 |
10,8 |
17,3 | |
|
0,3 |
1,2 |
5,4 |
11,3 |
18,8 | |
|
0,5 |
1,4 |
6.2 |
13,6 |
23,0 | |
|
0,7 |
1.5 |
7.5 |
16,3 |
28,6 | |
|
1.0 |
1.7 |
10,0 |
20,3 |
34,3 | |
|
1,25 |
2,0 |
11,5 |
23,0 |
37,8 | |
|
1,5 |
2,2 |
13,4 |
25,0 |
40,2 | |
|
2,0 |
2.2 |
14,2 |
27,0 |
43,1 | |
|
3,0 |
2,2 |
15,2 |
28,7 |
45,1 | |
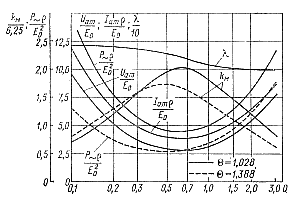
В табл. 5-3 приведены вычисленные значения относительных величин τ0, U1/E0, U2/E0, а на рис. 5-7 — зависимости Iаmρ/E0, Uam/E0, λ = ω1/ω0 и мощности в нагрузке Р~ρ/Е20 в функции Q для двух значений параметра Θ.
 |
С помощью выражения (1-5) нетрудно вычислить коэффициент kм, характеризующий использование тиристоров по мощности. Схемное время выключения тиристоров определяется выражением
где τ2 — безразмерное время, соответствующее моменту, когда существует условие u2 =0. |
Рис. 5-7. Зависимости для величин, характеризующих режим работы последовательно-параллельного инвертора с удвоением частоты
Вычисления показали, что произведение Θ (τ0—τв) лежит в диапазоне 1,55≤Θ (τ0—τ2) ≤1,64 при значительных изменениях параметров Θ и Q.
Поэтому с небольшой погрешностью, не более 5 %, можно принять Θ (τ0—τ2) ≈ π/2 и соответственно
kв≈ 1-1/(4Θ). (5-44)
Форма выходного напряжения может быть оценена коэффициентом гармоник, вычисляемым с помощью формулы
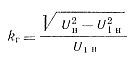
где Uн, U1н — действующие значения напряжения на нагрузке и его первой гармоники. Вычисленные значения kг также приведены в табл. 5-3.
Из приведенных на рис. 5-7 зависимостей видно, что величины Р~, Iam, Uam при Qопт = 0,4÷0,7 имеют минимум, a kм — максимум. При этом с увеличением Θ величины Р~ и kм уменьшаются.
Поскольку частота свободных колебаний ωх зависит от сопротивления r, то величина Qопт зависит от расстройки Θ. В табл. 5-4 даны вычисленные значения Qопт (Θ) и kм (Θ).
Таблица 5-4
|
Θ |
1,028 |
1,194 |
1,27 |
1,388 |
1,500 |
1,668 |
|
Qопт |
0,61 |
0,535 |
0,525 |
0,500 |
0,455 |
0,430 |
|
kм |
0,323 |
0,306 |
0,298 |
0,274 |
0,268 |
0,251 |
Таким образом, для наилучшего использования тиристоров по мощности следует рекомендовать режим при Qопт= 0,4÷0,7 с минимальными по возможности расстройками Θ.
Однако уменьшение Θ приводит к уменьшению коэффициента kв. Для получения минимальных коэффициентов kг следует расстройку Θ приближать к единице.
Сказанное позволяет сделать вывод, что оптимальным является режим при Qопт = 0,4÷0,7, Θ = 1,1÷1,3.
Расчет инвертора на максимальную мощность при заданной частоте и известных параметрах тиристоров следует производить в следующем порядке:
- Выбираем режим работы инвертора (т. е. величины Q и Θ), основываясь на приведенном выше анализе. Обычно целесообразно принимать Q = 0,4÷0,7; Θ = 1,1÷1,3.
- Полагая Uam = Ua.д и находя из рис. 5-7 отношение Uam/E0, определяем Е0.
- Определив из рис. 5-7 величину Iamρ/E0, c ее помощью находим ρ.
- Из рис. 5-7 находим λ = ω1/ω0.
- По известным ρ, Θ, λ = ω1/ω0 и Q нетрудно найти параметры схемы ω0 = ωΘ/λ, С = 1/(2ω0ρ), L = 1/(2ω20C), rн = ρ/Q.
- С помощью выражения (5-44) вычисляем коэффициент и проверяем соблюдение неравенства tв>tв.ном.
- Полагая импульсы тока через тиристоры синусоидальными, из формулы (5-10) находим величину Si и проверяем соблюдение условия Si ≤ Siд.



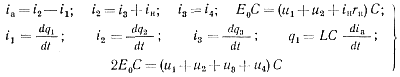
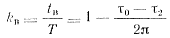 (5-43)
(5-43)