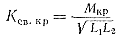Целью настройки связанных контуров в резонанс является получение наибольшего тока во втором контуре. Зависимость тока во втором контуре от частоты можно исследовать с помощью резонансных кривых двух связанных контуров. При индуктивной связи между и ток во втором контуре равен
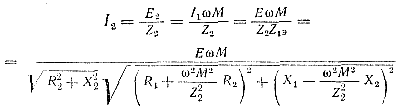
Обычно сначала настраивают первый контур при отключенном или разомкнутом втором, потом при слабой связи настраивают второй контур и подбирают оптимальную связь между контурами, обеспечивающую получение наибольшего тока I2макс.макс (максимум максиморум) во втором контуре. При настройке первого контура добиваются, чтобы Х1 = 0, а при настройке второго, чтобы Х2 = 0.
Тогда
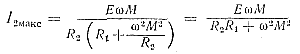 (166)
(166)
Для получения оптимального значения коэффициента взаимоиндукции Мопт, при котором ток во втором контуре достигнет величины I2макс.макс нужно взять производную и приравнять ее нулю:
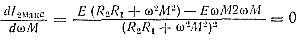
Приведя подобные члены в числителе и отбросив знаменатель (так как дробь равна нулю, когда числитель равен нулю, независимо от величины знаменателя, если только последний не равен нулю), легко найти
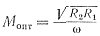
Подставив Mопт в формулу (166), получим
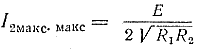
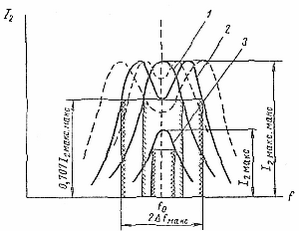 |
Различают три основных вида связи между контурами: критическую связь, связь ниже критической и связь выше критической. Из рис. 106 видно, что форма резонансной кривой связанных контуров и их полоса пропускания зависят от вида связи между контурами. При критической связи между индуктивно связанными контурами коэффициент связи равен
Рис. 106. Резонансные кривые связанных контуров. |
Если вместо Мкр подставить Мопт = √R2R1/ω0, то
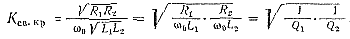
Для случая, когда можно предположить, что добротности обоих связанных контуров одинаковы, т. е. Q1 = Q2 = Q, Ксв = 1/Q. Резонансная кривая при критической связи между контурами соответствует форме резонансной кривой одиночного последовательного колебательного контура (см. рис. 100), но с более крутыми скатами и с полосой пропускания, большей в 1,41 раза, чем полоса пропускания одиночного контура.
При Ксв≈0,2Ксв.кр полоса пропускания связанных контуров равна полосе пропускания одиночного контура.
При связи много ниже критической (Ксв < 0,2Ккр) резонансная кривая имеет одногорбую форму, а полоса пропускания в этом случае оказывается меньше полосы пропускания одиночного контура.
При связи больше критической (Ксв > Ксв.кр) Резонансная кривая имеет двугорбую форму, полоса пропускания при этом становится еще шире, а скаты резонансной кривой — круче. Так, при Ксв≈2,4/Q провал резонансной кривой на частоте ƒ0 достигает ординаты 0,707I2макс.макс; а полоса пропускания оказывается примерно в три раза больше полосы пропускания одиночного колебательного контура. Дальнейшее увеличение связи приведет к еще большему расширению полосы пропускания. Однако на частоте ƒ0 и близкой к ней при прохождении сложного сигнала через систему связанных контуров появляются искажения составляющих сигнала, так как провал в резонансной кривой достигнет ординаты меньшей 0,707.
Таким образом, изменяя связь между контурами, можно изменять полосу пропускания связанных контуров.