Вынужденные колебания в параллельном контуре
На рис. 101, а представлен колебательный контур с параллельно включенными элементами L и С по отношению к приложенной э. д. с. (параллельный контур). Если частота ее совпадает с частотой свободных колебаний контура, то возникает резонанс токов.
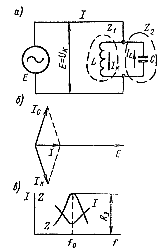 |
В этом случае, как видно из векторной диаграммы (рис. 101,б), токи в обеих ветвях контура равны между собой, так как равны друг другу полные сопротивления индуктивной (Z1) и емкостной (Z2) ветвей. Но при этом создаются сдвиги по фазе между токами и относительно приложенной э. д. с. Рис. 101. Вынужденные колебания в контуре с параллельно включенными элементами: а — схема включения; б — векторная диаграмма (резонанс токов); в — зависимость сопротивления контура и тока в питающем проводе от частоты. |
Из векторной диаграммы также следует, что ток I в неразветвленной части цепи при резонансе минимален, а стало быть, сопротивление максимально и активно (вектор тока / и вектор э. д. с. Е совпадают по фазе). Сопротивление, эквивалентное контуру при резонансе,
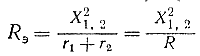
где r1, r2 — активные сопротивления соответствующих ветвей контура; X — реактивное сопротивление любой из них; R — полное активное сопротивление потерь.
Если Х1 и Х2 заменить их значениями, то можно получить формулу, устанавливающую связь между сопротивлением контура при резонансе и элементами контура:
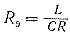 (155)
(155)
Следует отметить, что равенство реактивных сопротивлений обеих ветвей контура является достаточным условием для определения резонансной частоты ƒ0=1/2π√LC лишь при равенстве активных потерь в ветвях контура. Если активные потери в ветвях контура неодинаковы, то резонансная частота, определенная по приведенной выше формуле, должна быть скорректирована, т. е. контур следует подстроить.
Выразив индуктивность катушки в микрогенри, частоту в мегагерцах, а емкость контура в пикофарадах, получаем формулу, устанавливающую связь между этими величинами в следующем виде:
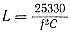
Определение добротности, приведенное ранее для последовательного контура, здесь не подходит, так как напряжение на элементах контура, независимо от его настройки, равно Uк(см. рис. 101, а). Физический смысл добротности для параллельного колебательного контура можно получить, приравняв следующие выражения, определяющие напряжение на контуре:
Uк = IRэ = Iкρ
откуда
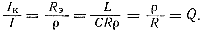 (156)
(156)
Добротность Q показывает, во сколько раз ток в контуре при резонансе больше тока в неразветвленной цепи.
На частотах ниже резонансной сопротивление индуктивной ветви меньше сопротивления емкостной ветви контура и, следовательно, ток в индуктивной ветви становится больше тока в емкостной ветви. Поэтому контур на частотах ниже резонансной, по отношению к источнику э. д. с, представляет собой индуктивную нагрузку.
На частотах выше резонансной картина становится противоположной и параллельный колебательный контур ведет себя как емкостная нагрузка.
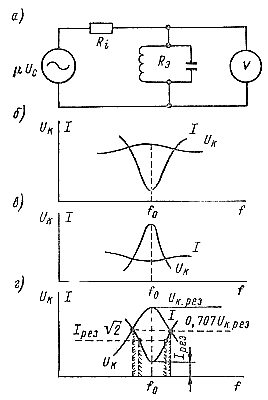 |
Параллельный колебательный контур обычно включают в анодную цепь лампы. При анализе такой схемы лампу заменяют эквивалентным генератором переменного тока с э. д. с, равной μUс (где Uс — напряжение входного сигнала на управляющей сетке лампы), с внутренним сопротивлением Ri (рис. 102, а). В зависимости от соотношения величин сопротивлений Ri и Rэ при резонансе, можно судить о настройке контура в резонанс либо по поведению тока в неразветвленной цепи, либо по поведению напряжения на зажимах контура. Рис. 102. Настройка параллельного контура: а — эквивалентная схема включения контура в анодную цепь электронной лампы; б — график I и Uк = φ (ƒ) при Ri<<Rэ; в — график I и Uк = φ (ƒ) при Ri<<Rэ; г — график I и Uк = φ (ƒ) при Ri<<Rэ. |
Ток в неразветвленной цепи равен
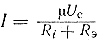
Напряжение на зажимах контура
Uк= I Rэ
Если Ri<< Rэ (что имеет место при включении контура в анодную цепь), то при настройке контура, в момент резонанса, ток в питающем проводе будет минимален, а напряжение на зажимах контура будет меняться незначительно. Так как по мере приближения к резонансу сопротивление контура растет, а ток в неразветвленной цепи падает, то произведение этих величин, представляющее напряжение на контуре, остается почти неизменным. Таким образом, в рассматриваемом случае судить о настройке контура в резонанс можно только по минимуму тока в питающем проводе (рис. 102, б).
Если Ri >> Rэ то, рассуждая подобным же образом, легко прийти к выводу, что при настройке контура ток в питающем проводе остается почти неизменным. Следовательно, о настройке контура в резонанс можно судить лишь по поведению напряжения на зажимах контура (рис. 102, в).
Особый интерес представляет третий случай, когда Ri и Rэ соизмеримы, т. е. Ri≈ Rэ. В этом случае о настройке контура в резонанс можно судить как по поведению напряжения па зажимах контура, так и по поведению тока в неразветвленной цепи (рис. 102, г).
Полоса пропускания параллельного контура по току может быть определена по формуле (153) для полосы пропускания последовательного контура лишь при Ri = 0. К этому же выводу можно прийти при определении полосы пропускания по напряжению при Ri = ∞:
2∆ƒ1 = ƒ0/Q при Ri = 0;
2∆ƒU
= ƒ0/Q при Ri→∞.
При Ri = Rэ полосы пропускания по току и по напряжению могут быть определены по формулам
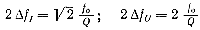
Полоса пропускания по напряжению получается шире полосы пропускания по току. Это объясняется тем, что внутреннее сопротивление генератора шунтирует контур, т. е. как бы увеличивает потери в нем. Поэтому иногда, для расширения полосы пропускания контура, его специально шунтируют сопротивлением. Дополнительные потери ∆r, вносимые в контур, определяются по формуле
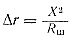 (157)
(157)
где X — реактивное сопротивление ветви контура; Rш — шунтирующее сопротивление. Добротность контура при учете влияния сопротивления шунта определяется формулой
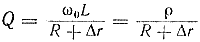
Известно, что наибольший ток в электрической цепи имеет место при равенстве внутреннего сопротивления источника и сопротивления нагрузки, поэтому при рассмотрении эквивалентной схемы, приведенной на рис. 102, а, можно сделать также вывод, что максимальный ток в цепи, а следовательно, и максимальное напряжение на зажимах контура и максимальная мощность в контуре, будут выделяться при Ri = Rэ. Значит, колебательный контур, включенный в анодную цепь лампы, должен быть не только настроен на частоту сигнала, но и представлять собой сопротивление, обеспечивающее наиболее целесообразный режим работы электронной лампы.
В связи с этим, в отличие от контура, представленного на рис. 102, a, называемого контуром первого вида, применяются колебательные контуры, в которых индуктивности или емкости распределены между ветвями контура. Они называются соответственно контурами второго и третьего видов (рис. 103, а, б). Настройка контура не изменится при любом перераспределении элементов L и С между ветвями контура при условии, что полные значения этих величин останутся неизменными.
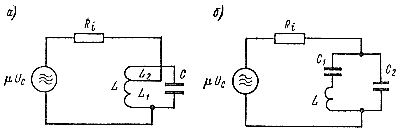 |
Так, например, если емкость конденсатора контура составляла 100 пф, то настройка контура не изменится при замене этой емкости двумя последовательно включенными в контур конденсаторами емкостью по 200 пф каждый. Рис. 103. Колебательные контуры второго (а) и третьего (б) видов. |
Иначе обстоит дело с сопротивлениями контуров второго и третьего видов при резонансе.
Рассмотрим контур второго вида, в котором индуктивность L распределена между ветвями контура. Сопротивление параллельного контура при резонансе, согласно определению, равно X21,2/R. В нашем случае Х1 = ω0L1, а не ω0L = ω0 (L1 + L2), как это было в контуре первого вида. Поэтому сопротивление контура второго вида при резонансе
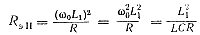
Умножим числитель и знаменатель на L, тогда
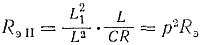 (158)
(158)
Коэффициент включения или коэффициент, учитывающий распределение индуктивности L между ветвями контура, р = L1/L<1, следовательно, сопротивление контура второго вида при резонансе меньше сопротивления контура первого вида.
К подобному же выводу можно прийти при рассмотрении контура третьего вида, сопротивление которого при резонансе
Rэ III=q2Rэ (159)
где q=С/С1<1 (так как С=C1C2/C1+C2)
Таким образом, перераспределяя индуктивность или емкость между ветвями контура, можно осуществлять переход от контура одного вида к контуру другого вида. Такой переход позволяет сохранять настройку неизменной, изменять сопротивление контура при резонансе и тем самым обеспечить его согласование (равенство) с внутренним сопротивлением электронной лампы.



