При амплитудной модуляции амплитуда высокочастотного модулируемого колебания изменяется в соответствии с изменениями амплитуды модулирующего колебания низкой частоты.
Рассмотрим основные теоретические соотношения для этого вида модуляции и практические способы ее осуществления.
Пусть высокочастотные колебания определяются уравнением
iω = Imω cos ωt,
где ω — угловая частота высокочастотного колебания, а колебания низкой частоты — уравнением
iω = ImΩ cos Ωt
где Ω — угловая частота низкочастотного колебания.
Тогда, согласно определению амплитудной модуляции, уравнение для модулированного тока можно написать так:
iм = (Imω + ImΩ cos Ωt) cos ωt.
Выражение в скобках определяет амплитуду высокочастотного колебания, изменяющуюся по закону изменения амплитуды колебания низкой частоты.
После несложных преобразований уравнение для модулированного тока примет вид
iм = Imω(1 +m cos ωt) cos ωt (388)
где m = ImΩ/Imω - коэффициент модуляции.
Рассуждая аналогичным образом, можно написать и уравнение для модулированного напряжения:
uм = Umω(l + m cos Ωt) cos ωt (389)
где
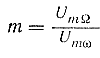
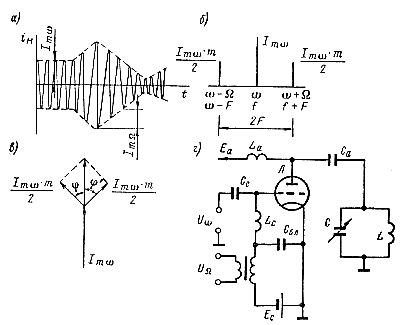 |
На рис. 201, а приведен график амплитудно-модулированного тока iм. Из графика видно, что коэффициент модуляции m не может быть больше единицы. Определим частотный состав амплитудно-модулированного колебания, пользуясь уравнением (388). Рис. 201. Амплитудная модуляция: а — график амплитудно-модулированного тока; б — спектр частот амплитудно-модулированного колебания; в — векторная диаграмма амплитудно-модулированного колебания; г — схема осуществления амплитудной модуляции. |
Раскрыв скобки и произведя несложное преобразование, получим
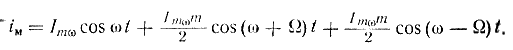
Из этого выражения следует, что при модуляции одним тоном с частотой Ω в состав модулированного тока входят три составляющие: составляющая основной — несущей частоты с амплитудой Imω и составляющие суммарной и разностной частот (верхней и нижней боковых частот) с равными амплитудами. Амплитуды боковых частот не могут быть больше половины амплитуды несущей.
На рис. 201, б показан спектр колебаний при амплитудной модуляции одним тоном. Модулированный сигнал при модуляции одной частотой Ω занимает в эфире полосу частот, равную удвоенной частоте модуляции (2Ω или 2F). На рис. 201, в приведена векторная диаграмма, иллюстрирующая процесс амплитудной модуляции. Мгновенное значение амплитуды модулированного тока (или напряжения) определяется геометрической суммой векторов амплитуд всех его составляющих.
Если составляющие модулированного тока были бы одной частоты, то взаимное расположение векторов их амплитуд в течение времени оставалось бы неизменным и, значит, амплитуда колебания была бы неизменной. В нашем случае вектор амплитуды тока составляющей верхней боковой частоты за время t опережает вектор амплитуды тока несущей частоты на угол φ = (ω + Ω) t; за этот же промежуток времени t вектор амплитуды тока составляющей нижней боковой частоты отстает от вектора тока несущей частоты на угол φ' = (ω — Ω) t; этот вектор как бы вращается в обратную сторону с частотой ω — Ω.
При модуляции спектром частот от Fмин до Fмакс в состав амплитудно-модулированного колебания входят не две боковых частоты, а две полосы боковых частот. Модулированный сигнал занимает теперь полосу частот, равную удвоенному значению наивысшей частоты модулирующего сигнала. Так, например, если модуляция осуществляется сигналами частот от 50 гц до 6 кгц, то независимо от несущей частоты амплитудно-модулированный сигнал занимает в эфире полосу частот П = 2Fмакс = 12 кгц.
Передаваемый сигнал содержится только в боковых частотах; несущая же частота в процессе модуляции никаких изменений не претерпевает. Поэтому практическое применение находит однополосная передача, когда передатчик излучает в эфир сигналы только одной боковой частоты. При этом сигнал занимает сравнительно узкую полосу частот, передатчик работает с более низким уровнем помех и с более высоким к. п. д.
Амплитудную модуляцию можно практически осуществить при помощи обычного усилителя мощности, на вход (на управляющую сетку) которого поступает высокочастотное напряжение несущей (модулируемой) частоты. Напряжение звуковой (модулирующей) частоты может быть приложено к любому электроду лампы, в том числе и к управляющей сетке.
В зависимости от того, к какому электроду приложено напряжение модулирующего фактора, изменяющего амплитуду высокочастотного тока, различают следующие схемы амплитудной модуляции:
- модуляции на анод;
- анодно-экранной модуляции;
- модуляции на защитную сетку;
- модуляции на экранирующую сетку;
- модуляции смещением на управляющую сетку.
Режим работы усилителя мощности, в котором осуществляется модуляция, определяется частотной и амплитудной модуляционными характеристиками.
Частотная модуляционная характеристика выражает зависимость коэффициента модуляции от частоты модулирующего напряжения при постоянной амплитуде и должна представлять собой прямую, параллельную оси абсцисс (оси частот).
Частотные искажения при модуляции отсутствуют, если коэффициент модуляции т не зависит от частоты, а определяется только соотношениями между токами звуковой и несущей частот. Следует иметь в виду, что в зависимости от схемы модуляции амплитуда модулирующего напряжения для получения заданного коэффициента модуляции т должна быть различной. Так, например, при осуществлении анодной модуляции амплитуда модулирующего напряжения должна быть во много раз больше, чем при модуляции на управляющую сетку, поскольку изменение напряжения на управляющей сетке в μ раз сильнее влияет на анодный ток.
Амплитудная модуляционная характеристика выражает зависимость коэффициента модуляции от амплитуды модулирующего напряжения при постоянной частоте. При отсутствии нелинейных искажений динамическая амплитудная характеристика должна представлять собой прямую, выходящую из начала координат под некоторым углом к оси абсцисс.
Значительный интерес представляет статическая модуляционная характеристика, которая устанавливает зависимость между первой гармоникой анодного тока или тока в контуре от изменения напряжения на электроде лампы, на который предполагается подавать в дальнейшем модулирующее напряжение. По статической модуляционной характеристике можно определить положение первоначальной рабочей точки (она должна находиться на средине линейного участка характеристики), исходное напряжение на управляющем электроде в режиме несущей частоты и амплитуду модулирующего напряжения, при которой нелинейные искажения не превышают допустимых.
В качестве примера на рис. 201, г приведена схема модуляции смещением на управляющую сетку. Одновременно на управляющую сетку поступают три напряжения: напряжение смещения от автономного источника Eс, напряжение несущей частоты Uω от возбудителя и модулирующее напряжение звуковой частоты UΩ.
В дополнение к изложенным выше требованиям, предъявляемым к режиму работы модулирующего каскада, следует заметить, что сеточная модуляция может иметь место лишь при изменении как величины максимального значения импульса анодного тока, так и угла его отсечки. Если модулирующий каскад будет работать без отсечки анодного тока, то перемещение рабочей точки вызовет лишь изменение постоянной составляющей анодного тока, но не его первой гармоники. Модуляция будет отсутствовать.
При амплитудной модуляции колебательная мощность, выделяемая в нагрузке, изменяется в широких пределах. Пределы изменения тока при модуляции можно определить из выражений
Iмакс = Imω(1 + m)
Iмин =
Imω(1 - m)
При модуляции мощность в нагрузке изменяется от величины
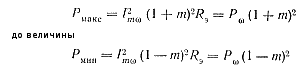
где Рω — мощность в режиме несущей частоты (при отсутствии модуляции); Rэ — сопротивление нагрузочного контура.
При m =1, Рмакс = 4Pω, а Рмин = 0.
Практический интерес представляет мощность, выделяемая в нагрузке за период модулирующего напряжения. Это так называемая телефонная мощность Рт:
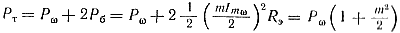
где Рб — мощность боковой частоты.
Из последнего выражения следует, что при модуляции в нагрузке выделяется мощность большая, чем в режиме несущей частоты. Поэтому режим несущей частоты при сеточной модуляции является наиболее тяжелым режимом работы лампы:
Ра=Р0-Рω≤Ра доп
Выбор лампы при модуляции смещением производят из условия
Рном≥Р
Лампы с оксидными катодами в максимальном режиме могут развивать мощность больше номинальной, поэтому при выборе лампы можно исходить из приближенного равенства
Рном≥(0.6÷0,7) Рмакс.
При амплитудной модуляции средняя мощность, получаемая от лампы, значительно меньше ее максимальной мощности, что является существенным недостатком амплитудной модуляции.



