При анализе процессов в тиристорных инверторах обычно принимают следующие допущения: пренебрегают активными сопротивлениями обмоток электромагнитных элементов, намагничивающими токами и собственными емкостями трансформаторов, используют кусочно-линейную аппроксимацию характеристик полупроводниковых диодов и тиристоров.
Однако даже при этих допущениях обобщенный анализ инверторов и генераторов является достаточно сложным.
Это обусловлено тем, что конфигурация их электрических цепей изменяется в течение каждого периода выходной частоты и процессы в этих устройствах описываются дифференциальными уравнениями достаточно высокого порядка.
Поэтому применение таких классических методов анализа, как методы разрывных функций, разностных уравнении, мгновенных значений, связано со значительными трудностями.
Наиболее приемлемы методы, базирующиеся на тех или иных способах численного интегрирования дифференциальных уравнений с использованием ЭВМ, что позволяет исследовать практически любые схемы.
При построении универсальных алгоритмов (цифровых моделей) тиристорных инверторов используем их топологические описании, позволяющие перевести графическую конфигурацию электронной схемы на алгебраический язык, с помощью которого составляются уравнения системы.
В основу топологического описания положен график схемы, а в качестве алгебраического языка взят аппарат топологических матриц — матрицы инциденций (структурной), матрицы контуров и сечений.
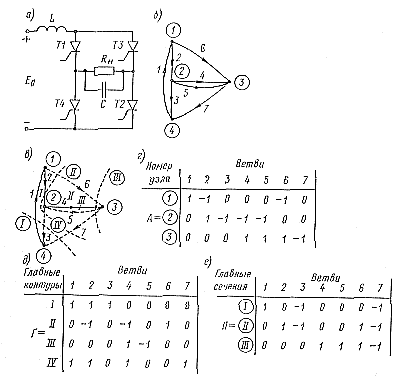 |
Рассмотрим такой подход на примере мостового параллельного инвертора, показанного на рис. 7-1, а. Там же (рис. 7-1, б) построен график данной схемы, в котором тиристоры T1—T4 замещаются эквивалентными активными сопротивлениями и лому двухполюсному компоненту схемы соответствует его символ — ветвь: 1 — L; 2 — Т1; 3 — Т4; 4 — Rн; 5 — С; 6 — Т3; 7 — Т2. Направление ветвей соответствует направлению передачи в них сигнала. На рис. 7-1, в построено дерево графа (сплошные линии), которое представляет собой совокупность ветвей 1—7, включающую в себя все узлы 1—4 (на рисунке эти цифры в кружках), но ни одного замкнутого контура. |
Рис. 7-1. Схема инвертора, ее граф и матрицы
В этом случае ветви 1, 2 и 4, вошедшие в дерево, называются ребрами графа, а ветви 3, 5, 6 и 7, не вошедшие в него,— хордами. На рис. 7-1, г, д, е приводятся соответствующие данной схеме топологические матрицы инциденций А, контуров Г и сечений П, которые формируются по известным правилам.
Конечная цель процесса оптимизации состоит в нахождении экстремумов целевых функций на множествах, определяемых линейными и нелинейными ограничениями.
Целевая функция есть такая характеристика, большему (или меньшему) значению которой соответствует лучшая с точки зрения искомого решения ситуация — в нашем случае наименьшее значение выбранного технико-экономического показателя.
Отметим, во-первых, что наша целевая функция является нелинейной, во-вторых, в ней невозможно аналитически отразить роль отдельных параметров устройства, например времени выключения тиристоров, и, в-третьих, существуют ограничения на технические параметры устройств.
Это позволяет считать целесообразным применение для решения данной задачи методов нелинейного программирования (НЛП).
В общем случае задача НЛП формируется следующим образом.
Если целевая функция F (х) непрерывна, функции h1 (x).....hm (x) задают ограничения в виде равенств, a gm+1(x),..., gp (x) — в виде неравенств, где вектор-столбец компонент в n-мерном пространстве X=[x1, x2,...,xn], то надо найти минимум функции F (х) при m линейных и (или) нелинейных ограничениях в виде равенств hj (х) = 0; j = 1...., m и (р—m) линейных и (или) нелинейных ограничениях в виде неравенств gi(x)≥0; j = m + 1.....р.
Под переменными x1 . . . , хn понимаются любые величины, характеризующие работу устройства, например электрические характеристики.
Целевая функция представляет собой тот или иной технико-экономический показатель, причем для его определения требуется знать соответствующие показатели каждого из элементов устройства (трансформаторы, дроссели, конденсаторы, диоды, тиристоры).
С этой целью вводятся так называемые критериальные модели, устанавливающие аналитические связи между основными параметрами и электромагнитными нагрузками элементов инверторов, с одной стороны, и их объемом (массой или стоимостью) — с другой.
Ограничениями являются математически сформулированные требования к характеристикам инверторов, определяемые техническим заданием на проектирование.



