Расчётные номограммы однотактного генератора

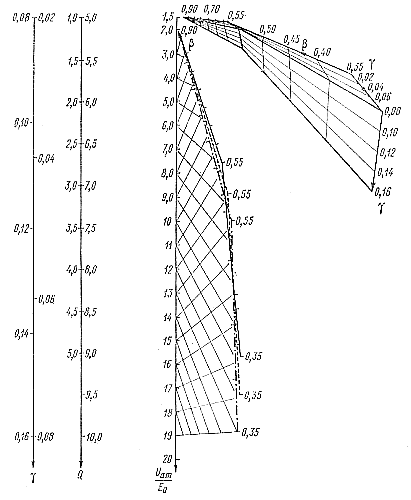
На рис. 2-15 приведена номограмма для величины Uam/E0. На ее примере рассмотрим методику построения номограмм для величин, являющихся функцией трех переменных. Следует отметить, что у большинства рассматриваемых далее инверторов и генераторов величины, описывающие режим работы, также являются функциями трех переменных, поэтому предлагаемая методика построения номограмм пригодна и для них. В данном случае используется номограмма из выравненных точек с параллельными равномерными шкалами Q, Uam/E0 и бинарным полем (β, γ), которое состоит на двух семейств прямых линий, образующих при наложении их друг на друга проективные шкалы.

Для ее построения применяется формула, полученная путем последовательной линейной интерполяции:

(2-47)

где Q₁, Q₂, β₁, β₂, γ₁, γ₂ — крайние значения независимых переменных; Q', β', γ' — текущие значения независимых переменных; U_аm11/Е₀÷U'_am22/Е₀— значения искомой функции, соответствующие крайним значениям независимых переменных.

Все они соответствуют табл. 2-2.

Анализ показывает, что если строить одну номограмму для всего диапазона значений Q, β, γ, то точность получится весьма невысокой, поэтому диапазон изменения каждой из этих величин разбивается на два примерно равных поддиапазона.

В результате получается восемь номограмм, которые могут быть построены на одном рисунке с помощью восьми таблиц (табл. 2-3— 2-10). Каждая из восьми номограмм состоит из двух параллельных равномерных шкал Q и U_am/Е₀ и бинарного поля с угловыми точками, соответствующими значениям β₁γ₁, β₂γ₁, β₁γ₂, β₂γ₂.

Угловые точки лежат на пересечении прямых, соединяющих значения величин Q и U_am/E₀, соответствующие параметрам β и γ, определенным из табл. 2-3—2-10. Например, точка, соответствующая значениям β₁, γ₁, лежит на пересечении линий, соединяющих точки Q₁, U_am11/E₀ и Q₂, U_аm/Е₀.

Поскольку диапазон изменения величины Q разбит на два поддиапазона, то для всех восьми номограмм используются две шкалы: 1≤Q≤5; 5≤Q≤10. На всех четырех сторонах бинарного поля строятся проективные шкалы.

Для их построения выбирается произвольная точка на шкале Q (обычно это одна из крайних точек шкалы). Из точки проводятся два луча через крайние точки стороны бинарного поля, на которой строится проективная шкала.

Далее правее этой стороны проводится прямая, параллельная шкалам Q и U_am/E₀. Она поресекает лучи в двух точках. На прямой, соединяющей эти точки, строится равномерная шкала, причем указанные точки соответствуют значениям величин на краях стороны бинарного поли.

Проецируя равномерную шкалу из выбранной точки Q на сторону бинаррого поля, получаем искомую проективную шкалу. Четыре номограммы для табл. 2-3—2-6 построены таким образом в верхней правой части рис. 2-15.

При построении номограммы может встретиться частный случай — вырожденное бинарное поле. Он получается, если четыре угловые точки бинарного поля оказываются практически на одной прямой.

В рассматриваемом примере это происходит для четырех номограмм при Q = 5÷10. Бинарное поле при этом заменяется двумя равномерными шкалами β, каждая — при постоянном значении γ, соответствующем угловой точке.

Таблица 2-2

 Таблица 2-3

Таблица 2-4

Таблица 2-5

Таблица 2-6

Таблица 2-7

Таблица 2-8

Таблица 2-9

Таблица 2-10

Искомое значение величины U_am/E₀ определяем следующим образом. Соединив заданную точку Q' с заданными точками на шкалах β, находим на шкале U_am/E₀ две точки U'_am/E₀ и U'_am/E₀. Затем строим шкалу параметра γ, либо совпадающую со шкалой Q, либо ей параллельную.

В рассматриваемом случае, поскольку диапазон изменения у разбит на два поддиапазона, удобнее построить две шкалы (рис. 2-15), Через крайние точки шкалы γ и точки U'_am/Е₀, U"_am/E₀ проводим прямые до их пересечения.

Соединив точку пересечения с заданным значением Q', определим искомое значение U_am/Е₀.

На рис. 2-15 для вырожденного бинарного поля построены сплошными линиями шкалы для табл. 2-7 и 2-8 и штриховыми — для табл. 2-9 и 2-10. Это соответствует значениям 0,02≤γ≤0,08 и 0,08≤γ≤ 0,16.

Так как диапазон изменения параметра γ разбит на два поддиапазона, то использованы две шкалы γ.

На рис. 2-15 для удобства пользования нанесена масштабная сетка, применяемая для диапазона 5≤Q≤10.