Анализ переходных процессов генераторов

В ряде практических случаев нагрузка тиристорного генератора представляется достаточно сложной эквивалентной схемой, состоящей из нескольких колебательных контуров (например, нагрузка в виде пьезокерамического преобразователя).

При анализе электрических переходных процессов для этих случаев в установившихся режимах можно воспользоваться результатами, полученными для более простых нагрузок и, в частности, чисто активной.

Для этого достаточно учесть влияние реактивной и активной составляющих нагрузки на коммутирующий контур генератора. При анализе переходных процессов такие упрощения невозможны.

Применение для такого анализа традиционных методов (мгновенных значений, разностных уравнений, разрывных функций и др.) либо приводит к значительным математическим трудностям и слишком сложным окончательным выражениям, либо требует использования ЭВМ для численного решения дифференциальных уравнений весьма высокого порядка.

Поэтому несомненный интерес представляет использование приближенных методов анализа, обеспечивающих в то же время необходимую точность и достаточно простые конечные выражения.

Эти методы в отличие от численных позволяют найти искомую величину в любой момент времени, не проходя временного интервала по шагам.

Погрешности определяются только приближениями, принимаемыми при выборе метода, и не зависят от размера шага интегрирования, как в численных методах.

Весьма перспективным является приближенный метод, предложенный для анализа переходных процессов в сложных линейных диссипативных RC- и RLС-цепях, напряжения и токи в которых при t→∞ стремятся к постоянным значениям.

Упрощение анализа достигается благодаря понижению порядка дифференциального уравнения, описывающего анализируемый процесс, и введению в полученное решение надлежащего запаздывания по времени.

Несмотря на то что в большинстве рассмотренных выше схем тиристорных инверторов и генераторов токи и напряжения носят колебательный характер и токи тиристоров в момент их выключения близки к нулю (токи удержания), использование указанного выше метода оказывается весьма эффективным.

Этому способствуют следующие обстоятельства.

Во-первых, используются приближенное выражение для тока во временном интервале длительностью около полупериода колебаний напряжения на нагрузке, т. е. используется область малых времен и сравнительно короткие промежутки времени.

Во-вторых, поскольку выключение тиристора происходит при токе i_a, меньшем тока удержания I_уд, но не при строго определенном его значении, то допустима погрешность определения момента перехода тока через нуль.

Полученное выражение (3-55) для преобразованного по Лапласу тока i_а (t) через один из тиристоров можно, вводя безразмерное время τ = ω_t, представить в виде, удобном для дальнейших преобразований:

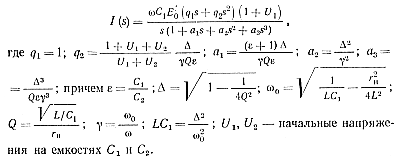(6-1)

В знаменателе выражения (6-1) стоит полином третьего порядка. Приближение первого порядка в этом случае не реализуется, так как запаздывающая функция, аппроксимирующая реальный процесс, является ступенчатой, и поскольку форма тока в нашем случае близка к синусоидальной, погрешность очень велика.

Можно показать, что приближение второго порядка реализуется в весьма узкой области значений параметров, определяющих режим работы схемы (например, при γ =1 и ε = 1 только для области l,5<Q<2).

Поэтому нужно искать аппроксимирующую функцию h_dm (m—порядок приближения) по способу производной.

В этом случае получается наилучшее приближение для искомых функций, имеющих колебательный характер.

В общем виде применительно к рассматриваемому инвертору избранный метод реализуется следующим образом.

Если изображение искомой функции имеет вид

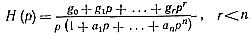(6.2)

то при g₀ = 0 или независимо от величины g₀ при невыполнении неравенств

а₁—g₁>0; а₂—g₂—g₁a₁>0; а₃—g₃—g₂a₁—g₁a₂>0

изображение аппроксимирующей функции можно искать в виде

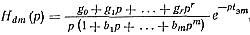(6-3)

где t_зm— время запаздывания аппроксимирующей функции.

Далее находим вспомогательную запаздывающую функцию h_зm(t), изображение которой

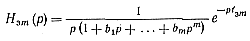(6-4)

представляет собой приближение h_зm~h функции с изображением

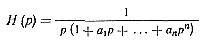(6-5)

Искомая аппроксимирующая функция имеет вид

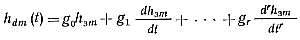(6-6)

В рассматриваемом случае

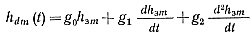(6-7)

где

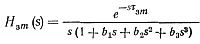(6-8)

Условием реализации приближения первого порядка является

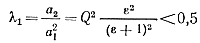(6-9)

Отсюда следует, что аппроксимирующая функция h_з1 реализуется при Q<0,7 для больших ε и при Q<√2 для ε = 1.

Условием реализации приближения второго порядка h_з2 является

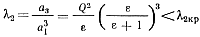(6-10)

Поскольку рекомендовались режимы при Q> 1 (обычно Q = 1÷3), то можно полагать в соответствии с (6-9) λ1>0,5, и тогда

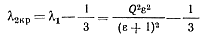
Условие (6-10) в этом случае имеет вид

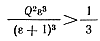(6-11)

Далее определяем время запаздывания, решая уравнение

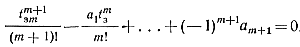(6-12)

Можно показать, что только один, наименьший вещественный (всегда положительный), корень этого уравнения выражает время t_вm.

Для рассматриваемого случая приближения второго порядка справедливо уравнение

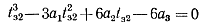(6-13)

Можно также показать, что имеют место соотношения:

0<t_зm<t_з(m-1)<. . .<t_з<t₃₀ = а₁, т. е. t₃₂<а₁.

Это же можно выразить формулой

t₃₂=(1-v)a₁(6-14)

где 0<v< 1.

Подставляя выражение (6-14) в (6-13), получим уравнение Кардана относительно v:

v₃+3rv + 2ƒ= 0,

где t = 2λ1-1; ƒ=1-3 λ1+3λ2

Если дискриминант D = ƒ₂+ r₃ больше нуля, что наверняка выполняется при λ1≥0,5, то единственный вещественный корень уравнения, определяющий запаздывание, есть

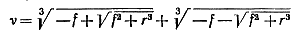(6-15)

Из выражения (6-14) следует

τ_з2 = a₁(l —v),

где v определяется уравнением (6-15).

Если выполнить условия r>0 и 40 ƒ²<27 r³, то, используя формулу Ньютона, получим

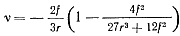(6-16)

Вычисления показывают, что указанные выше условия выполняются.

Коэффициенты в выражении (6-8) для Н_зт определяются с помощью формул:

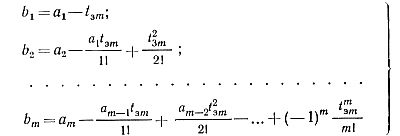(6-17)

В рассматриваемом случае достаточно использовать два первых коэффициента.

Взяв обратное преобразование от функции H_з2, получим

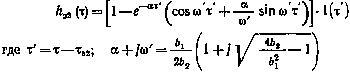(6-18)
 
Подставив выражение (6-18) в (6-7), окончательно получим

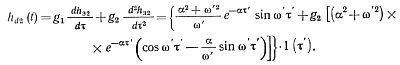(6-19)

Тогда для тока через тиристор получаем

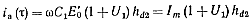(6-20)

Напряжения на емкостях С₁ и С₂ соответственно определяются выражениями:

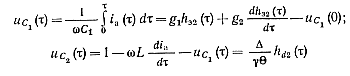(6-21), (6-22)

Таблица 6-1

Начальные значения напряжений u_C1 и u_C2 в k-м интервале проводимости тиристора, входящие в выражение для коэффициента g₂ и в выражение (6-2), определяются с помощью зависимостей (6-21) и (6-22):

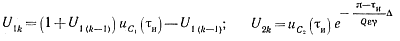
где τи - момент прекращения тока через тиристор в (k— 1)-м интервале проводимости, определяемый как наименьший отличный от нуля корень трансцендентного уравнения h_{d 2} (τи) = 0.

Результаты анализа переходных процессов, полученные точным и описанным выше приближенным методами, приведены в табл. 6-1.

Как видно из таблицы, длительности протекания токов через тиристоры весьма близки, а значения напряжений на емкости С, в моменты окончания интервалов проводимости для больших значений Q и ε совпадают с большой точностью.

Большие расхождения (до 15 %) получаются при вычислении максимальных значений тока тиристоров.

В целом полученные результаты для практического применения следует признать весьма удовлетворительными, причем эффективность изложенного приближенного метода возрастает но мере роста порядка дифференциальных уравнений, описывающих работу схемы, т. е. ее сложности.