Работа многоячейкового генератора

Поскольку нагрузкой многоячейковых генераторов является колебательный контур L_к, С_к, то в качестве ее параметров могут быть приняты эквивалентное сопротивление R_э и фазовый угол φ этого контура.

Для определения влияния нагрузки на работу многоячейкового генератора необходимо найти токи и напряжения в схеме как функции величин R_э и φ.

Выше были получены выражения (5-53), (5-60), (5-62), (5-64) — (5-66), (5-69) для величин U_am, i_a, U_Cp2, k_C, γ, I_1а, I_1р, I₀₁, характеризующих режим работы генератора в функции τ₁, ψ, v.

Чтобы получить перечисленные выше величины в функции R_э и φ, сначала надо найти зависимости τ₁ и ψ в функции R_э и φ, а затем, подставив τ₁ и ψ в указанные выражения, определим искомые зависимости.

Для определения функций τ₁(φ, R_э, v) и ψ (φ, R_э, v) используем выражения (5-66), вводя в них безразмерную амплитуду напряжения на контуре нагрузки

U=U_m/U_Cp1 (5-97)

Тогда величины I_1a и I_1p будут представлять собой функции четырех переменных:

I_1a=I_1a (U,τ₁, ψ, v); I_1p = I_1p (U, τ₁, ψ, v). (5-98)

Величина k_C (τ₁, φ, v) определяется из выражения (5-64), ζ— из 1 (5-46). Тогда

U (τ₁, ψ, v) = k_C(τ₁, ψ, v). (5-99)

Исключив из выражения (5-98) величину U, получим

I_1a= I_1a(τ₁, ψ, v); I_1p =  I_1p(τ₁, ψ, v). (5-100)

Представляя контур нагрузки в виде параллельного соединения активной G и реактивной в составляющих проводимости, получим общую проводимость контура нагрузки:

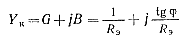(5-101)

где G=1/R_э; В=ωC_к-1/(ωL_к)=G tgφ=tgφ/R_э;  tgφ=I_1p/I_1a

Вводя для удобства дальнейших вычислений безразмерную величину первой гармоники тока через контур нагрузки I = πI₁ω_pL_p/U_Cp1, получим безразмерную проводимость:

Y'_к=-I/U=G'+jB'=-(g+jg tg φ) (5-102)

где g = 1 /R_э=πω_рL_p/R_э.Введение безразмерной величины g вместо R_э, удобно для построения зависимостей различных величин, характеризующих работу генератора, от параметров нагрузки.

Знак минус в уравнении (5-102) появляется вследствие того, что выражения для величин I и U получаются в результате решения уравнения эквивалентной схемы генератора, где пассивная цепь (контур нагрузки) заменена активной.

Представляя, с одной стороны, модуль проводимости Y'_к через величины g и tg φ, а с другой — через безразмерные величины I и U, получим

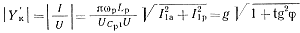(5-103)

Сравнивая левую и правую части уравнения (5-103) и учитывая зависимость tg φ = I_1p/I_41a, получим два уравнения для нахождения токов I_1а и I_1р:

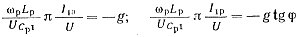(5-104)

Отсюда с учетом известной из выражения (5-97) величины U определяем токи:

I_1a = I_1a (R_э, φ, ψ, τ₁, v); I_1p = I_1p(R_э, φ, ψ, τ₁, v). (5-105)

Сравнивая выражения (5-105) и (5-100), получаем уравнения:

I_1a (τ₁, ψ, v)= I_1p(R_э, φ, ψ, τ₁, v) (5-106)
I_1p (τ₁, ψ, v)= I_1p(R_э, φ, ψ, τ₁, v)

С их помощью находим

ψ = ψ(τ₁,  R_э, v); φ = φ(τ₁,  R_э, v),  (5-107); (5-108)

причем выражение (5-108) представляет собой в неявном виде зависимость

τ₁ = τ₁(R_э, φ, v). (5-109)

Используя выражения (5-107) и (5-109), можно определить зависимости k_С (φ, R_э, v); ζ (φ, R_э, v) и γ (φ, R_э, v).

Чтобы получить удобные для численных расчетов математические выражения, вычислим интегралы (5-66):

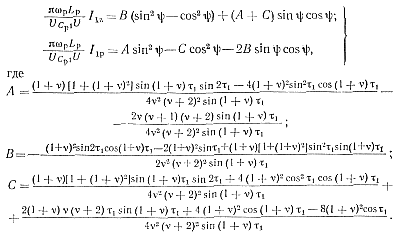(5-110)

 Приравняв правые части выражений (5-104) и (5-110), получим

-g=B(sin²ψ-cos²ψ)+(A+C)sinψcosψ
g tg φ=A sin₂ψ-C cos²ψ-2B sin ψ cosψ (5-111)

Исключив из уравнений (5-111) ψ, получим уравнение относительно φ:

g² tg² φ + (А - С) g tg φ + g²-B²—AC = 0. (5-112)

Его решением будет

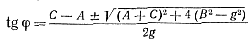(5-113)

Величину tg ψ найдем из выражения (5-111):

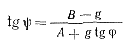(5-114)

или

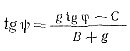(5-115)

Выражения (5-113), (5-114) или (5-115) позволяют определить зависимости τ (R_э, φ, v); ψ (R_э, φ, v).

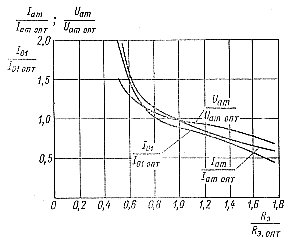
Подставляя полученные значения τ1 и ψ в уравнения (5-64), (5-62), (5-60), (5-65), (5-53), (5-69), находим зависимости kC (Rэ, φ, v); ζ (Rэ, φ, v); Iam (Rэ, φ, v); γ (Rэ, φ, v); Uam(Rэ, φ, v); I01 (Rэ, φ, v). Эти зависимости вычислены для оптимального режима. На рис. 5-18 и 5-19 приведены теоретические зависимости изменения токов через тиристоры и напряжений на их анодах по сравнению с оптимальным режимом.

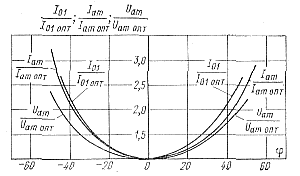Величины  Uam опт,  I01 опт, Iam опт соответствует оптимальному режиму. Полученные зависимости позволяют сделать следующие выводы:

Рис. 5-19. Зависимости для величин I_am/I_{am опт}, U_am/IU_{am опт}, I₀₁/I_{01 опт}.

1. При изменении фазового угла φ, т. е. при расстройке контура нагрузки, токи и напряжения генератора изменяются по резонансным кривым, что следует учитывать при расчете. Зависимость ζ (φ) имеет также резонансный характер с максимумом при φ = 0. Благодаря этому при расстройке генератор работает устойчиво, поскольку напряжение на анодах тиристоров остается отрицательным после их выключения.
2. Поскольку значение ζ увеличивается с ростом R_э и уменьшается с уменьшением Rэ, то условие устойчивой работы генератора нарушается при возрастании Rэ.
3. Зависимости напряжений и токов тиристоров от сопротивления R_э показывают, что при увеличении R_э токи и напряжения тиристоров уменьшаются, но при этом возникает условие ζ>₁ и может нарушиться устойчивость работы генератора. При уменьшении R_э токи и напряжения тиристоров возрастают, что необходимо учитывать при расчете генератора.