Расчёт генератора на одном тиристоре

При анализе работы генератора с учетом сопротивления нагрузки R_н в процессе решения дифференциальных уравнений, описывающих работу схемы, получаются алгебраические уравнения четвертой степени общего вида, аналитическое решение которых громоздко.

Поэтому при достаточно добротном контуре нагрузки решение задачи с необходимой для практического использования степенью точности можно получить, пренебрегая сопротивлением R_н. Уравнения четвертой степени становятся при этом биквадратными.

В результате решения дифференциальных уравнений, описывающих работу схемы, преобразованное по Лапласу выражение для тока через тиристор i_a имеет вид

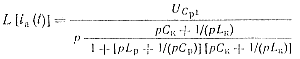 (2-1)

Вводя обозначения ω_к=1/√L_кС_к; n₁=L_p/L_к; m₁=C_p/C_к, получим

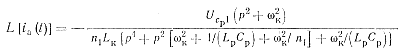(2-2)

Трехчлен знаменателя выражения (2-2), заключенный в фигурные скобки, представим в виде (р² + а²₁ω²_к)к) (р² + β²₁ω²_к), где

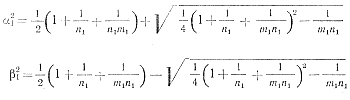(2-3), (2-4)
Тогда выражение (2-2) примет вид

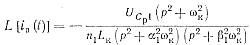 (2-5)

Преобразованное по Лапласу напряжение u_к на контуре L_к, С_к определяется выражением

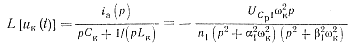(2-6)

Применяя обратное преобразование Лапласа к выражениям (2-5), (2-6) и вводя безразмерное время τ= ω_кt, находим

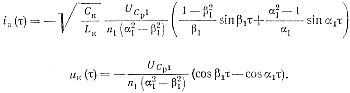(2-7), (2-8)

Из выражений (2-7) и (2-8) следует, что ток тиристора и напряжение на контуре L_к, С_к в процессе разряда емкости С_р имеют две составляющие с разными частотами.

В момент τ = τ₁ = ω_кt₁ ток i_a (τ₁) принимает нулевое значение, тиристор выключается и разрядная цепь L_p, С_р оказывается разомкнутой. Колебания с момента τ₁ происходят только в контуре L_к, С_к.

Амплитуду напряжения для первого периода этих колебаний U_m нетрудно вычислить следующим образом. Энергия колебательного контура W_к в любой момент времени складывается из магнитной энергии индуктивности и электрической энергии емкости.

Для момента τ₁ можно записать

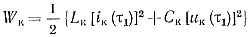(2-9)

С другой стороны, так как при анализе сопротивлением R_н мы пренебрегли, энергия колебательного контура выражается через амплитуду напряжения на нем:

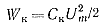  (2-10)

Из выражений (2-9) и (2-10) получаем

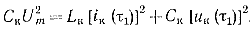  (2-11)

Используя (2-8), найдем контурный ток в момент выключения тиристора:

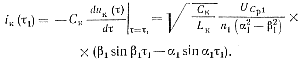(2-12)

Учитывая выражения (2-8) и (2-12), из (2-11) окончательно получаем

(2-13)

В зависимости от выбора соотношений параметров разрядной цепи L_p, С_р и контура нагрузки L_к, С_к, можно получить различные режимы работы генератора. Наилучшим с практической точки зрения (в дальнейшем назовем его оптимальным) будем считать режим, отвечающий следующим требованиям.

Во-первых, амплитуда напряжения первого периода колебаний в конуре нагрузки U_m равна абсолютному значению напряжения |UС_р2| перезаряда емкости С_р, т. е.

ξ = U_m/|UC_p2| = l. (2-14)

При условии ξ>1 отдаваемая контуру нагрузки мощность возрастает. Однако такой режим неприемлем, поскольку возможны преждевременные отпирания тиристора в моменты максимумов напряжения на контуре, когда напряжение на аноде становится положительным, а тиристор еще не успевает выключиться.

Режим при условии ξ<1 энергетически невыгоден, так как амплитуда колебаний U_m напряжения u_к и соответственно мощность в контуре нагрузки меньше, чем при ξ = 1.

Во-вторых, напряжение на разрядной индуктивности L_p в момент окончания импульса тока через тиристор равно нулю:

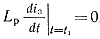(2-15)

При этих условиях напряжение на аноде тиристора после окончания импульса тока изменяется плавно, без скачков, вызывающих паразитные колебания в цепи L_p, С_р.

Эти колебания недопустимы, поскольку приводят к дополнительным потерям, перенапряжениям на элементах этих цепей и аноде тиристора, а также к повышению вероятности преждевременного отпирания тиристора при появлении положительного напряжения на его аноде.

Используя выражения (2-7) для тока i_а, (2-13) для напряжения U_m и находя из (2-3) и (2-4)

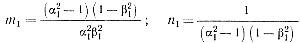(2-16; 2-17)

с помощью условий (2-14) и (2-15) получим два уравнения для определения величин α₁, β₁, τ₁ соответствующих оптимальному режиму работы генератора:

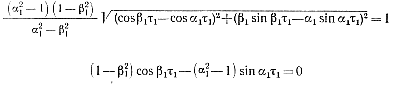(2-18), (2-19)

Третье уравнение можно получить, полагая ток iа равным нулю в момент t₁ окончания тока через тиристор:

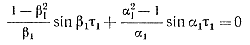  (2-20)

Решая уравнения (2-18) — (2-20) и используя (2-16), (2-17), находим m₁ = 9/16, n₁ = 25/9, τ₁ = 284,5° для оптимального режима работы.

Приравнивая нулю производную от тока i_а, получаем уравнение для определения безразмерного времени τм, при котором ток достигает максимального значения:

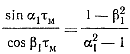(2-21)

Для оптимального режима τ_м = π/2.

Подставив значение τ_м  в уравнение (2-7), находим максимальный ток через тиристор I_am. Для оптимального режима выражение для I_am имеет следующий простой вид:

I_am = 0,37UС_р1С_кω_к. (2-22)

Если пренебречь потерями в индуктивности L_з, то усредненное за период следования импульсов тока через тиристор напряжение на ней должно быть равно нулю, откуда

Е₀ = (UC_р1+Uс_р2)/2, (2-23)

Выражение (2-23) позволяет установить связь между величиной Е₀ и напряжением на емкости С_р при отпирании тиристора. Поскольку выражение для напряжения uC_p (τ) = 1/Cp∫ia(τ) dτ на емкости С_р при ее разряде в соответствии с (2-7) равно

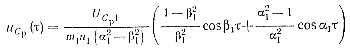(2-24)

то, подставив в него соответствующие значения величин α₁, β₁,m₁, n₁ и τ = τ₁, для оптимального режима найдем

Uc_p2=-0,6UC_p1

Теперь из (2-24) видим, что

E₀ = (UC_p1-0,6UC_pl)/2=0,2UC_p1(2-25)

Ранее указывалось, что после окончания протекания тока через тиристор к его аноду прикладывается отрицательное напряжение емкости С_р и колебательное напряжение на контуре нагрузки u_к.

Если предположить, что напряжение u_к затухает достаточно быстро, то схемное время выключения tв определяется только напряжением на емкости С_р. В течение времени заряда емкости С_р напряжение на ней изменяется по законуформула (2-26)

где Ωз = 1/√L_зC_p — собственная частота контура L_з, С_р (индуктивностями L_p и L_к пренебрегаем, поскольку они много меньше величины L_з).

Приравняв напряжение uC_p(t) нулю, находим

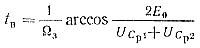(2-27)

Для оптимального режима Ω_зt_в = 75,5°≈0,42 π

Расчет генератора на максимальную мощность по заданным характеристикам тиристоров, приведенным в конце первой главы, при заданной частоте колебаний в нагрузке ƒ= 1/Т удобно производить в следующем порядке:

1. Полагая U_a.д равным максимальному напряжению на аноде тиристора U_am, которое, в свою очередь, равно UC_pl, а также I_amд=I_am и зная, что генерируемая частота ƒ равна частоте собственных колебаний контура нагрузки ƒк, из выражения (2-22) находим емкость С_к.
2. Определяем величину L_к. Так какƒ_к = ƒ, то L_k = 1/(ω2_кС_к) .
3. По известным отношениям С_р/С_к = m₁, L_р/L_к=n₁ находим соответственно С_р и L_p.
4. Выражение (2-25) позволяет определить напряжение источника питания Е₀.
5. Полагая t_в = t_в.ном, находим Ω_з = 0,42 π/t_в.ном и затем L_з = 1/(Ω²₃С_р).

В ряде случаев оказывается, что период следования импульсов тока через тиристор больше периода собственной частоты цепи заряда Ω_з. При этом для предотвращения обратного разряда емкости С_р на источник питания последовательно с индуктивностью L_з включается диод.

В схеме рис. 2-1 генерируемая частота практически не ограничивается номинальным временем выключения тиристоров t_в.ном. Однако недостатком схемы является увеличение с ростом частоты ƒ потерь в тиристоре, связанных с инерционностью процессов его включения. Это объясняется следующим.

С одной стороны, ток через тиристор, длительность которого определяется собственной частотой контура нагрузки L_к, С_к и соотношением параметров разрядного контура и контура нагрузки, с увеличением генерируемой частоты нарастает все более круто.

С другой стороны, время, в течение которого напряжение на тиристоре падает до сравнительно малых значений, от частоты не зависит и остается неизменным. Мощность потерь при включении, определяемая произведением тока и напряжения тиристора, в результате этого увеличивается.

В конечном счете это ведет к уменьшению КПД, мощности, получаемой от одного тиристора, и использование рассматриваемых схем на частотах свыше 100—150 кГц (для лучших типов современных тиристоров) неэффективно.