Связанные контуры - два контура называются такв том случае, если электрические процессы, происходящие в одном из них оказывают влияние на электрические процессы, происходящие в другом.
Простейшей и, вместе с тем, наиболее распространенной является индуктивная (трансформаторная) связь между контурами (рис. 104, а). Э. д. с. Е, подключенная к первому контуру, создает в нем ток I1. Около катушки индуктивности L1 образуется переменное магнитное поле, которое наводит в катушке L2 э. д. с. взаимоиндукции.
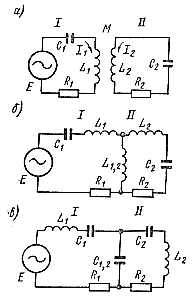 |
Во втором контуре появляется ток I2, создающий около катушки L2 переменное магнитное поле, которое, в свою очередь, наводит э. д. с. взаимоиндукции в первом контуре. Так как катушки L1 и L2 находятся на некотором расстоянии друг от друга, то часть магнитных силовых линий катушки L1 замыкается в окружающем пространстве, не достигая катушки L2. Степень влияния контуров друг на друга оценивается коэффициентом связи Ксв. В случае индуктивной связи между контурами он показывает, во сколько раз э. д. с, наводимая во втором контуре, меньше той э. д. с, которая могла бы быть в нем наведена, если бы все магнитные силовые линии катушки L1 участвовали в ее создании. Рис. 104. Схема связанных контуров: а —- индуктивная связь; б—автотрансформаторная связь; в — емкостная связь. |
Таким образом, коэффициент связи всегда меньше единицы:
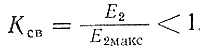
Изменяя расстояние между катушками, можно менять величину коэффициента Ксв. В ряде случаев это изменение связи между контурами осуществляют, поворачивая одну катушку относительно другой, при фиксированном расстоянии между катушками. При индуктивной связи
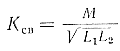 (160)
(160)
Формула (160) примет более общий вид, если числитель и знаменатель умножить на ω:
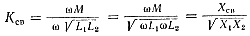 (161)
(161)
Итак, коэффициент связи между контурами определяется отношением сопротивления связи (Хсв) к корню квадратному из произведения одноименных реактивных сопротивлений контура (индуктивных или емкостных).
На рис. 104, б показана система связанных контуров при так называемой автотрансформаторной связи между контурами, когда взаимное влияние контуров друг на друга осуществляется через катушку индуктивности L1,2, одновременно входящую в оба контура. В этом случае сопротивление связи Хсв = ωL1,2, одноименные реактивные сопротивления контуров Х1 и Х2 соответственно равны со (L1 + L1,2) и со (L2 + L1,2). Подставив значения Хсв, X1 и Х2. В формулу (161), после несложных преобразований получим, применительно к рассматриваемому случаю автотрансформаторной связи, выражение для коэффициента связи:
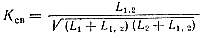 (162)
(162)
Как следует из формулы (162), связь между контурами тем больше, чем больше индуктивность L1,2.
При емкостной связи между контурами взаимное влияние их друг на друга осуществляется через конденсатор C1,2, одновременно входящий в оба контура (рис.104, в). При определении коэффициента связи, так же как и ранее, напишем выражения для Хсв, X1 и X2:
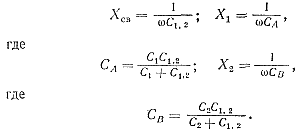
Подставив эти значения в формулу (161), получим, применительно к рассматриваемому случаю емкостной связи, выражение для коэффициента связи:
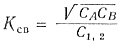 (163)
(163)
Приведенные три способа связи между контурами являются наиболее простыми. В практике применяются и другие, более сложные, комбинированные виды связи. Для удобства анализа работы связанных контуров их обычно заменяют одиночным эквивалентным контуром. При этом все выводы, сделанные применительно к одиночному контуру, распространяют на любую сложную систему связанных контуров.
В качестве примера рассмотрим случай индуктивной связи между контурами (см. рис. 104, а). Воспользовавшись вторым законом Кирхгофа, можно написать следующие уравнения:
E = I1R1 + I1jX1 +
I2jXсв
0 = I2R2 +
I1JX2 + I2jХсв.
Решив второе из приведенных уравнений относительно тока I2 и подставив его значение в первое уравнение, получим
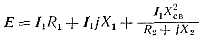
После несложных преобразований имеем:
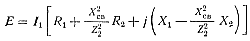 (164)
(164)
Здесь выражение в квадратных скобках представляет собой сопротивление эквивалентного контура Z1э, т. е. сопротивление первого контура с учетом влияния на него второго контура;
R1 — активное сопротивление первого контура; 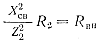 — вносимое активное сопротивление
из второго контура в первый; Х1 — реактивное
сопротивление первого контура;
— вносимое активное сопротивление
из второго контура в первый; Х1 — реактивное
сопротивление первого контура; 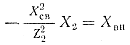 — вносимое реактивное сопротивление из второго
контура в первый.
— вносимое реактивное сопротивление из второго
контура в первый.
Таким образом, систему связанных контуров можно заменить эквивалентным последовательным контуром в виде последовательного соединения активного и реактивного сопротивлений эквивалентного контура:
Z1э=R1э+jX1э
Ток в первом (эквивалентном) контуре можно определить по формуле
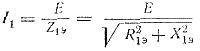 (165)
(165)
Влияние второго контура на первый заключается в увеличении активных потерь в первом контуре и в изменении его реактивного сопротивления. Активное сопротивление эквивалентного контура всегда больше активного сопротивления первого контура, а реактивное сопротивление эквивалентного контура зависит от знаков Х1 и Х2. Резонанс в эквивалентном контуре (в связанных контурах) наступает при Х1э = 0.
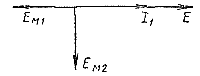
Взаимное влияние контуров можно объяснить и при помощи векторной диаграммы, приведенной на рис. 105.
|
|
|
Векторная диаграмма построена для случая, когда оба контура настроены на частоту э. д. с, приложенной к первому контуру, т. е. резонансная частота первого контура ω01, равна резонансной частоте второго контура ω02 и обе они совпадают с частотой внешней э. д. с. Рис.105. Векторная диаграмма связанных контуров. |
Из векторной диаграммы видно, что ток в первом контуре совпадает по фазе с внешней э.д. с. Это объясняется тем, что сопротивление настроенного в резонанс контура имеет активный характер. Ток I1 наводит э. д. с. взаимоиндукции в катушке L2:
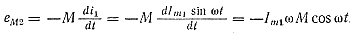
Так как
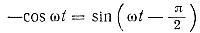
то
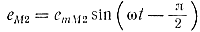
Из последнего выражения следует, что ЕМ2 отстает по фазе от I1 на 90°. Ток во втором контуре I2 наводит в первом контуре э. д. с. взаимоиндукции ЕМ1 которая отстает по фазе от тока на 90°.
Из векторной диаграммы также видно, что внешняя э. д. с. E и э. д. с. взаимоиндукции ЕМ1 находятся в противофазе. Последнее вызывает уменьшение тока в первом контуре:
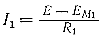
так как внешней э. д. с. приходится преодолевать встречную э. д. с. ЕМ1.
К подобному же выводу легко можно прийти, воспользовавшись формулой (165).
Действительно, когда оба контура настроены в резонанс, т. е. когда X1 = 0 и Х2 = 0, ток в первом контуре
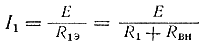
Влияние второго контура на первый сказывается в форме увеличения сопротивления первого контура на величину вносимого сопротивления Rвн, что вызывает уменьшение тока в первом (эквивалентном) контуре.
Условие резонанса для случая индуктивной связи между контурами можно записать так:
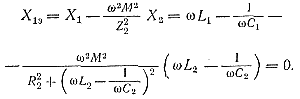
Если пренебречь R2, то реактивное сопротивление эквивалентного контура будет равно
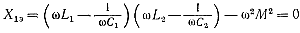
После несложных алгебраических преобразований и замены С1 через 1/L1ω20 , С2 через и 1/L2ω20 через K2св, уравнение для Х1э в окончательном виде принимает вид
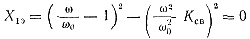
Это уравнение относительно частоты со имеет два корня:
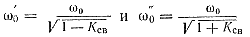
Из последних выражений следует, что эквивалентный контур, а стало быть и система связанных контуров, имеет две частоты, соответствующие резонансу, при которых ток в эквивалентном контуре получается наибольшим. Чем больше связь между контурами, тем больше ω'0 (ƒ'0) и ω''0 (ƒ''0) отличаются от резонансной частоты, па которую настроен каждый из контуров в отдельности.